Transistor linearly digitizes airflow

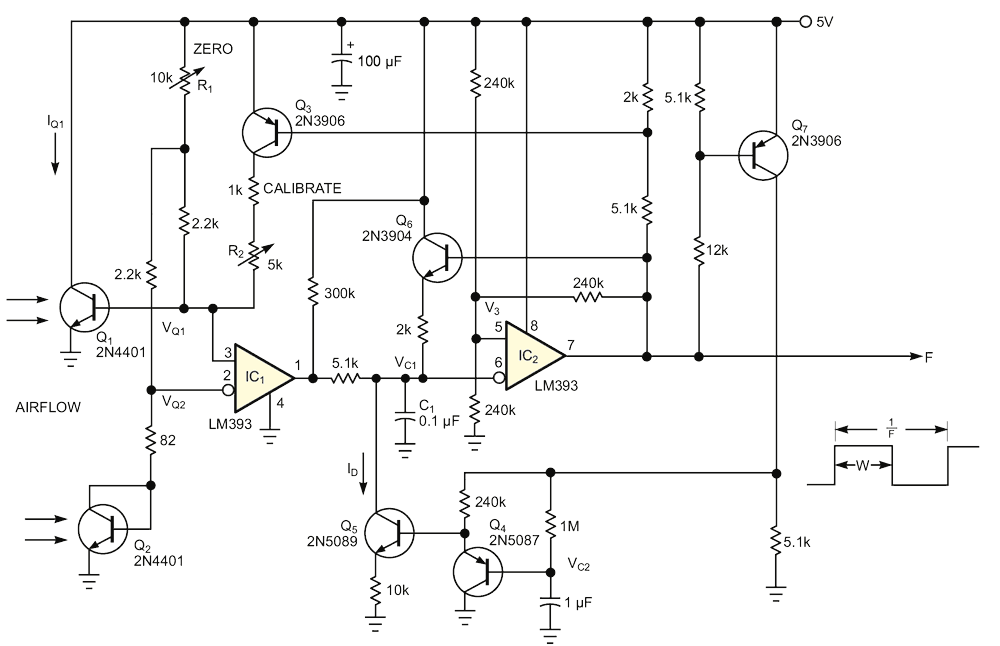
A sensitive and reliable way to measure airflow is to take advantage of the predictable relationship between heat dissipation and air speed. The principle of thermal anemometry relies on King's Law, which dictates that the power required to maintain a fixed differential between the surface of a heated sensor and the ambient air temperature increases as the square root of air speed. The popular hot-wire anemometer exploits this principle, but it suffers from the disadvantage of using a specialized and fragile metallic filament, the hot wire, as the airflow sensor. The circuit in Figure 1 avoids this disadvantage by using a pair of robust and inexpensive transistors instead of a flimsy wire for air-speed sensing. The Q₁/Q₂ front end of the circuit borrows from an earlier Design Idea (Reference 1). Just as in the 1996 circuit, the circuit in Figure 1 works by continuously maintaining the condition V_Q1 = V_Q2. To perform this task, the circuit must keep Q₁ approximately 50 °C hotter than Q₂.

Figure 1.	Using a simple transistor as sensor, this circuit yields a digitized, linear measurement of air speed.

V_BE balance requires this temperature difference, because Q₁'s collector current, I_Q1, is 100 times greater than that of Q₂, I_Q2. If Q₁ and Q₂ were at the same temperature, this ratio would result in V_Q1's being greater than V_Q2 by approximately 100 mV. Proper control of I_Q1 establishes differential heating that makes Q₁ hotter than Q₂. The method thus exploits the approximate –2-mV/°C temperature coefficient of V_BE to force V_Q balance. The resulting average, I_Q1, proportional to the average power dissipated in Q₁, is the heat-input measurement that forms the basis for the thermal air-speed measurement. Calibration of the sensor begins with adjustment of the R₁ zero-adjust trim. You adjust R₁ such that, at zero airflow, V_Q1 = V_Q2 with no help from Q₃. Then, when moving air hits the transistors and increases the heat-loss rate, V_Q1 increases and causes comparator I_C1 to release the reset on C₁. C₁ then charges until I_C2 turns on, generating a drive pulse to Q₁ through Q₃.

The resulting squirt of collector current generates a pulse of heating in Q₁, driving the transistor's temperature and V_BE back toward balance. Proper adjustment of R₂ calibrates the magnitude of the I_Q1-induced heating pulses to establish an accurate correspondence between pulse rate and air speed.

Now, consider measurement linearization. The square-root relationship of King's Law makes the relationship between heat loss and air speed nonlinear. You must iron the kinks out of the air-speed-calibration curve. You might achieve linearization in software, of course. However, depending on the flexibility of the data system the anemometer works with, a software correction is sometimes inconvenient. Another earlier Design Idea (Reference 2) presented an analog solution to linearization. But if you want the advantages of a digital, pulse-mode output – that is, noise-free transmission over long cable runs – you need a different fix.

The circuit in Figure 1 provides both linearity and a digital output. The average heat the pulses deposit in Q₁ is

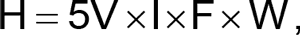
where I is the amplitude of the Q₁ current pulses (adjusted with R₂), F is the output frequency, and W is the pulse width. W is inversely proportional to I_D, the discharge current that ramps down V_C1 and controls the on-time of I_C2. Q₄ and Q₇ average the output duty cycle to generate a control voltage for Q₅ and thus make W a function of F. In fact, the feedback loop this arrangement establishes implicitly makes

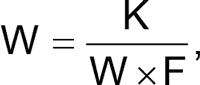
where K is a calibration constant determined by the component values. Therefore,

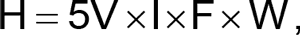
and

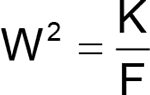
This expression yields

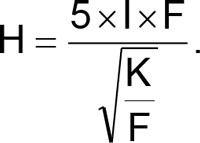
making F the desired function of H² and thus linearizing the relationship between frequency and air speed.

References

1. Woodward, Steve, "Self-heated transistor digitizes airflow," EDN, March 14, 1996, pg 86.
2. Woodward, Steve, "Transistor and FVCs make linear anemometer," EDN, Sept 26, 1996, pg 72.

Materials on the topic