Pierre Mars, CAP-XX Ltd, Australia
EDN
Small wireless sensors are becoming ubiquitous. Applications for sensors include building control, industrial control, security, location tracking, and RFID. It is much more convenient and cost-effective to autonomously power these sensors with a small energy-harvesting source without expensive wires or batteries that need repeated replacement.
The environment provides infinite ambient energy, including piezoelectric, thermal, vibration, and photovoltaic energy, but at low power, which falls short of the peak power necessary for transmitting data across wireless networks such as IEEE 802.15.4 (Zigbee), 802.11 (WLAN), or GSM/GPRS. A battery or a supercapacitor acts as a power buffer to store enough energy to provide the power bursts needed to acquire and transmit data. These energy-storage devices charge at low power and deliver the burst power when necessary.
Sizing the supercapacitor
Supercapacitor cells typically operate at 2.3 to 2.8V. The most efficient and cost-effective strategy is to limit the supercapacitor’s charge voltage to less than the cell-rated voltage and store enough energy for your application.
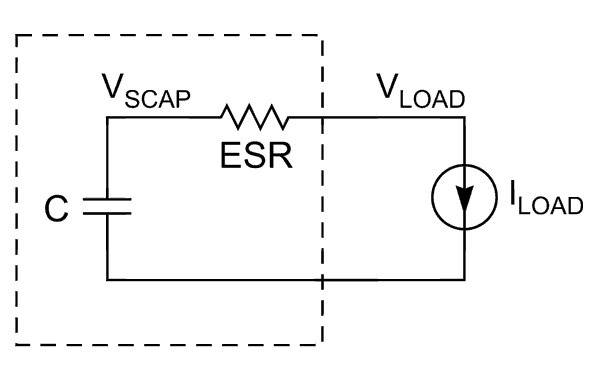 |
|
| Figure 1. | Ideal supercapacitor model; capacitance in series with ESR. |
A simple approach to sizing the supercapacitor is to calculate the energy necessary to support the peak power of the application, P, and set this value equal to
![]()
where
C is the capacitance,
V2INITIAL is the square of the supercapacitor’s voltage just before the peak-power burst,
V2FINAL is the square of the final voltage.
However, this equation does not allow for any losses in the supercapacitor’s ESR (equivalent series resistance). The load sees a voltage
VINITIAL−ESR×ILOAD,
where
ILOAD is the load current.
Because the load voltage decreases, the load current increases to achieve the load power. Referring to Figure 1, designers can model supercapacitor discharge as
![]()
where VSCAP is the supercapacitor’s voltage.
This equation yields the equation for the load current:
![]()
Supercapacitor discharge can then be simply modeled in Excel as
![]()
![]()
![]()
This calculation is important if the load current times ESR is significant compared with the supercapacitor’s final voltage. In this case, a simple energy-balance approach would make the supercapacitor’s value too small. This undersizing is likely to be the case at low temperatures, when ESR is typically two to three times higher than at room temperature.
The supercapacitor capacitance and ESR should also allow for aging. Supercapacitors slowly lose capacitance and increase ESR over time. The aging rate depends on cell voltage and temperature. Designers should select initial capacitance and ESR so that the end-of-life capacitance and ESR can support the applications.
Supercapacitor charging
A discharged supercapacitor looks like a short circuit to an energy source. Fortunately, many energy-harvesting sources, such as solar cells and microgenerators, can drive into a short circuit and directly charge a supercapacitor from 0V. ICs to interface energy sources, such as piezoelectric or thermoelectric energy, must be able to drive into a short circuit to charge a supercapacitor.
The industry has invested much effort in MPPT (maximum-peak-power tracking) to most efficiently draw power from energy-harvesting sources. This approach is applicable when charging a battery that must charge at constant voltage. The battery charger is typically a dc/dc converter that is a constant-power load to the energy source, so it makes sense to draw that power at the most efficient point using MPPT.
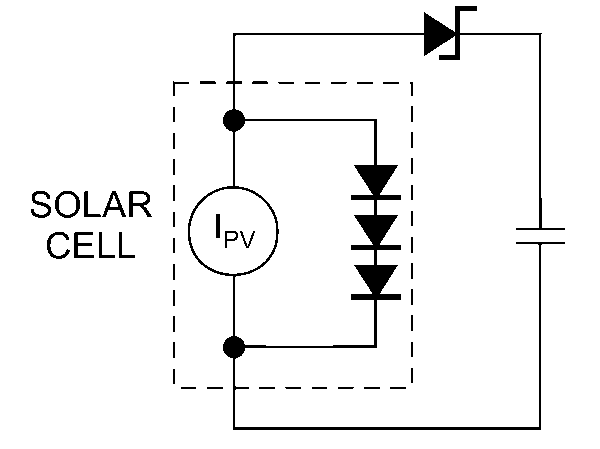 |
|
| Figure 2. | This simple and effective charging circuit targets use in cases in which the open-circuit voltage of a solarcell array is less than the supercapacitor’s rated voltage. |
In contrast to a battery, a supercapacitor need not charge at a constant voltage but charges most efficiently by drawing the maximum current the source can supply. Figure 2 shows a simple and effective charging circuit for cases in which the open-circuit voltage of a solar-cell array is less than the supercapacitor’s rated voltage. The diode prevents the supercapacitor from discharging back through the solar cell if it goes dark. If the energy source’s open-circuit voltage is greater than the supercapacitor’s voltage, then the supercapacitor requires overvoltage protection using a shunt regulator (Figure 3). A shunt regulator is an inexpensive and simple approach to overvoltage protection, and, once the supercapacitor fully charges, it does not matter whether the excess energy dissipates.
The energy harvester is like a hose with an endless supply of water filling a barrel, which is analogous to a supercapacitor. If the hose is still running once the barrel is full, the water may overflow. This situation differs from that of a battery, which has a limited energy supply and thus would require a series regulator.
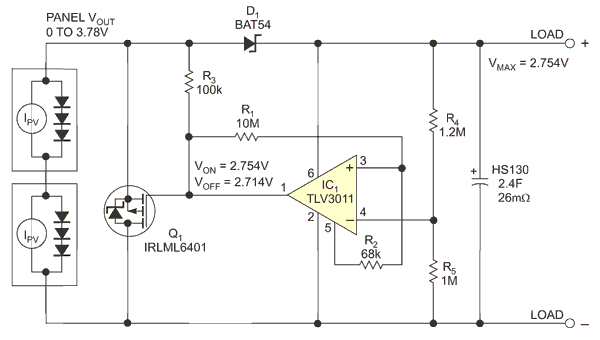 |
|
| Figure 3. | If the energy source’s open-circuit voltage is greater than the supercapacitor’s voltage, then the supercapacitor requires overvoltage protection using a shunt regulator. |
In the circuit in Figure 2, the supercapacitor, at 0V, draws short-circuit current from a solar cell. As the supercapacitor charges, the current decreases, depending on the solar cell’s voltage/current characteristic. The supercapacitor always draws the maximum current it can, however, so it charges at the highest possible rate. The circuit in Figure 3 uses the TLV3011 comparator because it integrates a voltage reference, draws only approximately 3-μA quiescent current, and is an open-drain cell so that the output is open-circuit when the regulator is off. This circuit uses the BAT54 diode because it has a low forward voltage at low currents – that is, the forward voltage is less than 0.1V at a forward current of less than 10 μA.
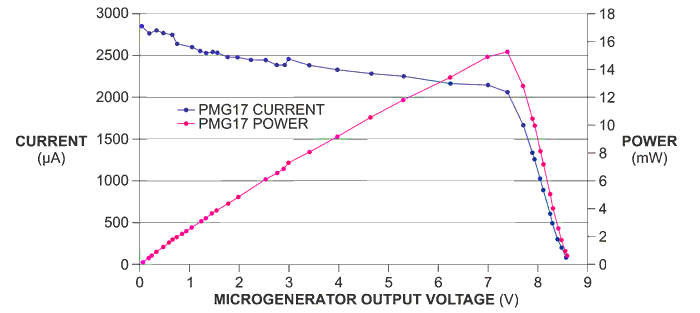 |
|
| Figure 4. | The voltage-current characteristic of a microgenerator is similar to that of a solar cell and delivers maximum current into a short circuit. |
Microgenerators are ideal for industrial-control applications, such as monitoring rotating machinery, because by definition they will vibrate when they are operating. Figure 4 shows the voltage-current characteristic of a microgenerator, which is similar to that of a solar cell and which delivers maximum current into a short circuit. A microgenerator also includes a diode bridge, which prevents the supercapacitor from discharging back into the generator, leading to a simple charging circuit (Figure 5).
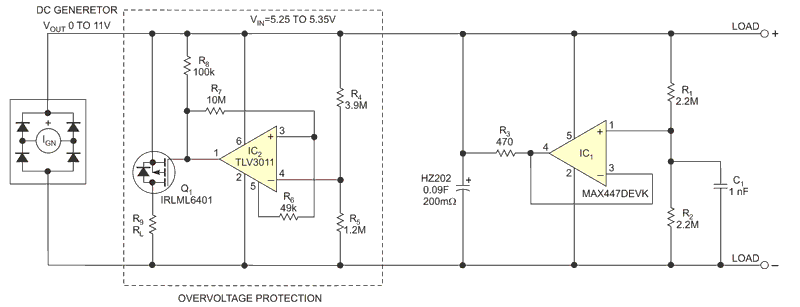 |
|
| Figure 5. | A microgenerator includes a diode bridge, which prevents the supercapacitor from discharging back into the generator, leading to a simple charging circuit. |
The open-circuit voltage is 8.5V, requiring a dual-cell supercapacitor, such as the CAP-XX HZ202, which operates at 5.5V. A shunt regulator provides overvoltage protection, and a lowcurrent active-balance circuit ensures even distribution between the cells. Linear Technology, with its LT3652l, LTC3108, and LTC3625 ICs, and Texas Instruments, with its BQ25504, charge supercapacitors from energy-harvesting sources.
Leakage current
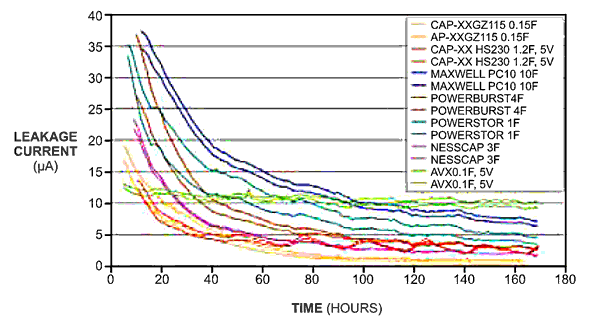
Because some energy harvesters deliver only a few microamps, leakage current becomes important. Supercapacitors can have leakage currents of less than 1 μA, making them suitable for energy-harvesting applications (Figure 6).
 |
|
| Figure 6. | A rule of thumb for equilibrium-leakage-current CAP-XX supercapacitors at room temperature is 1 μA/F. |
When a supercapacitor charges, the leakage current decays over time as the ions in the carbon electrodes diffuse into the pores. The leakage current settles to an equilibrium value, which depends on capacitance, voltage, and time. Leakage current is proportional to cell capacitance. A rule of thumb for equilibrium-leakage-current supercapacitors at room temperature is 1 μA/F. The 150-mF capacitors in Figure 6 have leakage currents of 0.2 and 0.3 μA after 160 hours. Leakage current increases exponentially with temperature. The time it takes to settle to the equilibrium value decreases with increased temperature as the ions diffuse more rapidly. Thus, these capacitors require a minimum current to charge from 0V. Depending on the supercapacitor, this current ranges from 5 to 50 μA. Designers should consider testing the minimum charging current when selecting a supercapacitor for an energy-harvesting circuit.
Cell balancing
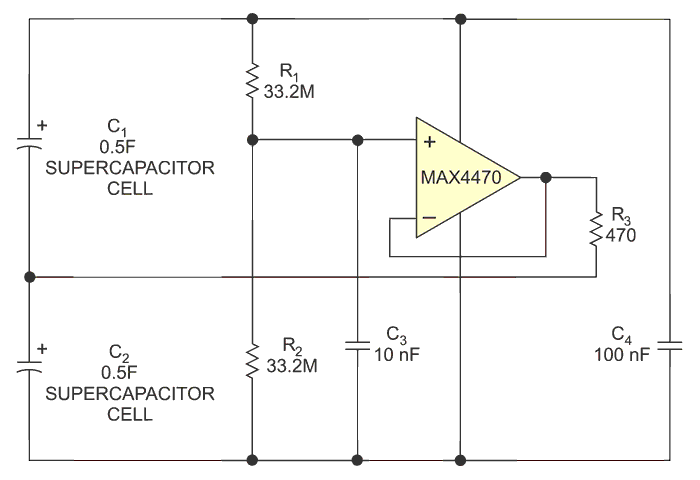
Circuits requiring that the supercapacitor’s terminal voltage is greater than the cell-rated voltage require several supercapacitor cells in series to reach the rated voltage, such as 5V or 12V. In this case, a cell-balancing circuit is necessary; otherwise, one of the cells could go into an overvoltage condition because the cells all have slightly different leakage currents, with different voltage-to-leakage-current characteristics. Because they are in series, however, they must all have the same leakage current. To achieve this goal, the cells redistribute charge among themselves; in doing so, one cell may go into an overvoltage state. Cells at varying temperatures or aging over time at different rates can exacerbate this problem. The simplest balancing circuit is a resistor in parallel across each cell. Depending on the leakage current of the supercapacitor and the operating temperature, the resistor’s value typically ranges from 1 to 50 kΩ, but the leakage current through the balancing circuit is too high for most energy-harvesting applications. A better approach for energy-harvesting applications is to use a low-current active-balance circuit (Figure 7).
 |
|
| Figure 7. | Low-current active-balance circuits target use in energy-harvesting applications. |
The MAX4470 op amp in the figure has a supply current of 750 nA and a rail-to-rail input and output. R3 limits the output current in the event that one cell causes a short circuit. The resulting design draws 2 to 3 μA after 160 hours of balancing a 0.5F CAP-XX HW207 supercapacitor.
Temperature performance
A major advantage of supercapacitors for energy-harvesting applications is their wide temperature performance. Examples include powering location-tracking units using vibration transducers, which may be operating in subzero temperatures, or solar panels in winter sunlight. Supercapacitor ESR at –30°C is typically two to three times ESR at room temperature, so the device can still deliver peak power even at low temperatures. In contrast, the internal impedance of thin-film batteries may reach several kilohms at such low temperatures.
Complementing batteries
In some applications, supercapacitors are alternatives to batteries; in others, they support them. In some situations, a supercapacitor may be unable to store sufficient energy, necessitating the use of a battery. For example, when the ambient-energy source – the sun, for example – is intermittent, as it would be at night, then the device must store energy not just for peak-power delivery but also to support the application for an extended time. If the needed peak power exceeds the amount the battery can supply – for GSM calls or low-power transmission in cold temperatures, for example – then the battery can charge the supercapacitor at low power, and the supercapacitor can deliver the high power bursts. This arrangement also means that the battery never cycles deeply, extending battery life. Supercapacitors store energy by physical-charge storage, not chemically as in batteries, so supercapacitors have an effectively infinite cycle life.
When a supercapacitor charges from a battery to supply peak-power bursts, there is a critical interval between bursts where if the bursts arrive more often, then it is more energy-efficient to always leave the supercapacitor on charge. If the bursts arrive less often, however, it is more energy-efficient to charge the supercapacitor just before the peak-power event. This interval depends on several factors, including the charge that the supercapacitor absorbs before reaching equilibrium leakage current, the self-discharge characteristic of the supercapacitor, and the charge the circuit draws from the supercapacitor to supply the peak-power event. This choice is available only if you know beforehand when the peak-power event will occur, and that is not possible if it is in response to an unpredictable event, such as battery failure or an external stimulus.
