Most of us know about PWM DACs. They are easy to implement, cheap, and acceptable for low performance applications.
The approach is to filter the HF components of the PWM signal and be left with only the LF or DC component that is proportional to duty cycle. However, the low-pass filter can’t filter out the PWM frequency completely, and for that reason, the LF/DC signal will generally have some ripple.
There are two approaches to decrease the ripple of a PWM DAC. You can lower the cut-off frequency of the low-pass filter, or increase the frequency of PWM signal. Inevitably, lower cut-off frequency translates to slower rise-time, and faster PWM frequency translates to lower resolution when achieved by reducing the counter size at a given clock frequency.
I am going to talk about an interesting Design Idea that focuses on lowering the ripple of PWM DACs without using the methods discussed above.
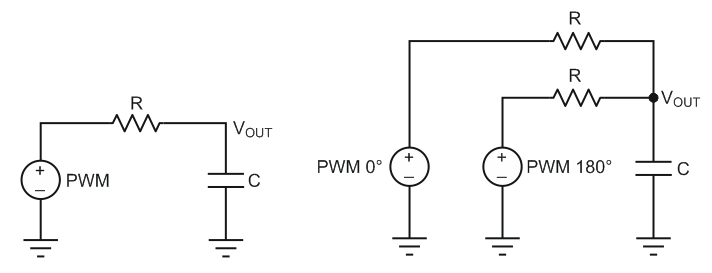
It turns out we can lower the ripple by using two PWM signals which have 180° phase difference between them (Figure 1). Intuitively, when there is 180° phase difference between two sinusoidal signals at the same frequency, they cancel each other out, so we expect the harmonics to cancel each other out when we use two PWM signals with 180° phase difference between them, right? Well, it is true, but not for all harmonics of the PWM signals. Some of them get cancelled, but some of them don’t. It has to do with the Fourier series and it’s a little too involved for this post, so I won’t go into the math.
 |
||
| Figure 1. | Single and dual-PWM circuits | |
How is a 180° phase shift between two PWM signals implemented? I used TI’s MSP430FR5969 LaunchPad, but the approach is mostly generic. In order to implement phase shift you are going to need two timers. One of the timers has to have two Compare-capture-PWM (CCP) modules and the other one needs only a single CCP.
You use one of the CCPs to set the PWM frequency and duty cycle in the timer that has two CCPs, and the other one to generate an interrupt to start the other timer with a delay that is equal to a half of period of the PWM. A single CCP in the other timer is used to set to the same PWM frequency and duty cycle. You are also going to have to “fine tune” the delay because software is going to introduce extra time between PWM signals. For example, in line 102 of my code, I changed the compare register value from (timer_period+1)/2 to (timer_period+1)/2-27.
I did a little bit of research to see if other microcontrollers have similar hardware and the capability to implement the method I used: Many Atmel microcontrollers have more than one timer and usually each has two CCPs (for instance, ATmega 328). Therefore it should be possible to implement this method. Another popular example, the STM32F051R8 (that's the microcontroller that some of the popular ST boards use) has 11 timers, and many of them have more than one CCP. Texas Instrument’s ARM based microcontrollers usually have separate PWM and timer modules (for example, TM4C123GH6PM), so it should be easier to implement phase shift. Two PWM modules can be started with a delay of half the PWM period by using one of the timers.
At VOUT of the phase-shift DAC, two PWM signals are summed together and hopefully some of the harmonics cancel each other out so we end up with lower ripple.
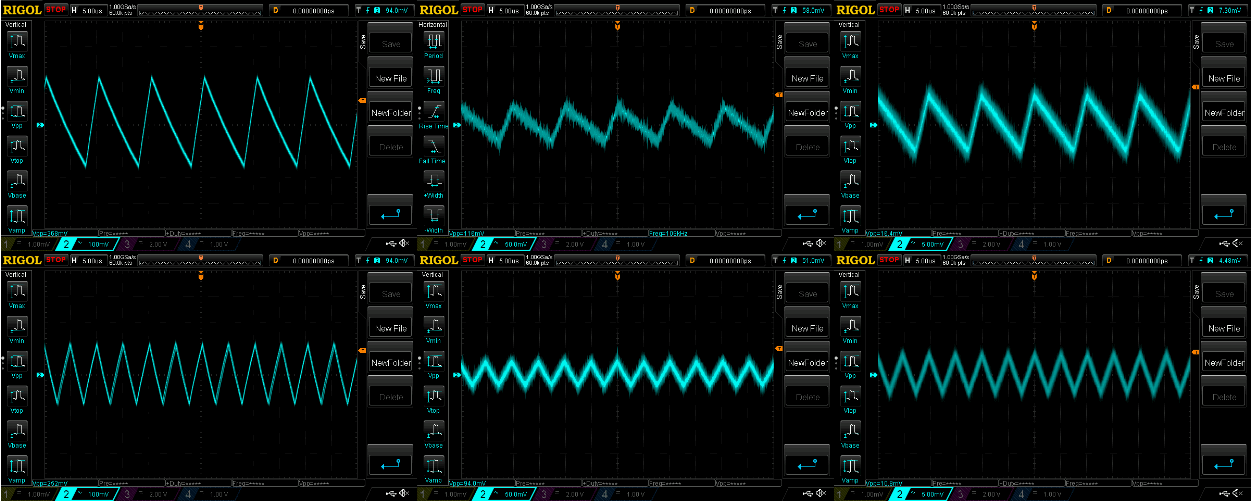
Let’s look at three cases using different resistor values (Figure 2). Each PWM signal is 100 kHz at 25% duty cycle.
|
||||||||
| Figure 2. | The upper traces are the conventional PWM. The lower are the dual, phase-shifted PWM. Volts/div. decreases from left to right: 100 mV, 50 mV, 5 mV. |
|||||||
By looking at the results we observe two things. First, peak-to-peak ripple is lowered. Second, the ripple’s fundamental frequency for the conventional PWM DAC is equal to the PWM signal’s frequency (100 kHz). The ripple’s fundamental frequency for the phase shift PWM DAC is equal to the second harmonic of the PWM signal (200 kHz), which means we successfully eliminated the first harmonic of the PWM signal with the phase shift DAC.
One advantage of this method is lower ripple without increased rise time (or the same ripple at half the rise time).
Another potential advantage is a doubling of the DAC’s effective resolution by setting the two PWMs one count apart to obtain an intermediate value. This does incur a slight asymmetry and increased ripple, but the effect is negligible.
