The human eye is remarkably sensitive to changes in light level. In ambient light ranging over several orders of magnitude, the eye can detect changes of only a few percent, yielding an incredible dynamic range. The primary trick is that the eye’s response to stimulus is logarithmic rather than linear. Thus, a doubling of the light level evokes much the same response in the eye whether it happens in a dimly lit room or in direct sunlight.
Photodiodes and phototransistors, whether photoresistive or photovoltaic, respond to a wide range of light levels by producing a current (not voltage) that is, unfortunately, linearly proportional to the light (as long as you keep the voltage bias constant or nearly so). We have to do something additional to obtain the desired logarithmic behavior. Fortunately, a logarithmic relationship is hidden in the humble PN junction.
Applying a forward bias across a bipolar junction causes a current to flow that is exponential with the voltage. For example, the datasheet for the ZLLS400 Schottky diode shows that at room temperature, the forward current changes by a factor of approximately 1.035 for each millivolt change in forward voltage. But saying that the current is exponential with voltage is just another way to say the voltage is logarithmic with current. This relationship allows a diode to be combined with an optical sensor to create a sensing circuit with an eye-like response.
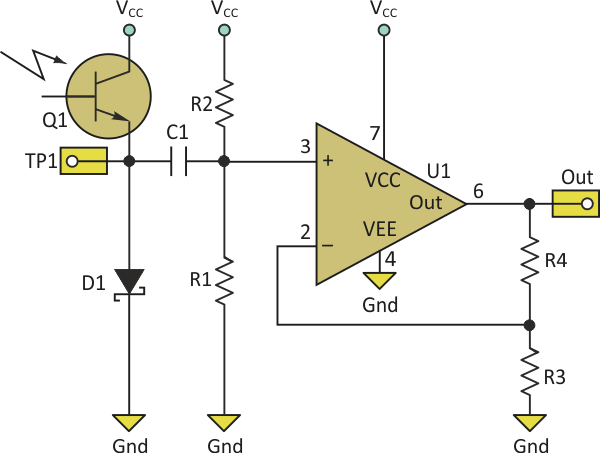
The circuit needed is deceptively simple (Fig. 1). The diode (D1) biases the phototransistor with a voltage that is just a tiny bit less than VCC over a huge range of operating conditions. This arrangement yields a voltage output at TP1 that is proportional to the logarithm of the incident light level as desired. Unfortunately, it is a very low signal level.
 |
||
| Figure 1. | The voltage across a PN junction has a logarithmic relationship to the current through it, allowing this optical sensor circuit to mimic the human eye’s sensitivity to changes in light level over a wide range of ambient levels. |
|
Suppose you have an application that needs to determine whether a light or a dark object passes in front of the sensor and that the “light” object reflects 80% of the ambient light, while the “dark” object reflects 20% – a 4:1 contrast ratio. The difference between the two objects would produce a voltage change of approximately 30 mV at TP1.
Significant changes in ambient light can change the signal’s base level by 10 times this amount or more. But the change in base level may not present a major challenge if the ambient light level always changes relatively slowly, while the signal of interest changes much more quickly. In such cases you can simply ac-couple (highpass filter) the output and then apply gain.
The circuit shown can use a range of component values to generate responses that suit different applications. Unfortunately, the component selections interact to some degree. The place to start is setting the amplifier’s gain. In the example application of a 4:1 contrast ratio and thus a 30-mV swing, suppose further that you want a 3-V swing at the output, perhaps from 1 to 4 V to stay comfortably clear of the supply rails. This requires a gain of approximately 100 in the amplifier. Thus, R4 should be 99x R3. For most practical purposes, R3 = 1 kΩ and R4 = 100 kΩ would suffice nicely.
Next, decide where the output should settle during steady-state conditions. If the quiescent state of the application has the sensor looking into a light background for detecting the passage of dark objects, for instance, the steady-state output should be near the positive rail to allow maximum swing in the negative (dark) direction when an object passes by. (You are, of course, using a modern rail-to-rail opamp for U1.) If you choose for the output to settle at about 4 V then, with the gain of 101, the op-amp input would need to settle to 4 V/101 = 39.6 mV.
The op amp’s steady-state voltage is
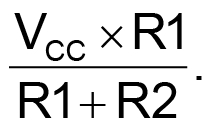
Assuming VCC = 5 V and working backward, R2 must be 125.25 × R1. To have a fairly high impedance at this point, a good combination might be R2 = 10 MΩ and R1 = 78.7 kΩ (nearest standard 1% value to the ideal 79.84 kΩ).
If the application has a dark background as the steady-state condition for detecting lighter objects, simply change the desired steady-state voltage in the calculation above from 4 to 1 V and repeat the calculation, arriving at 20 kΩ (19.8 kΩ) for R1.
Once the values for R1 and R2 are available, set the high-pass filter cutoff frequency. Suppose that the ambient light level can change over seconds to minutes, while the changes of interest would happen on the order of 100 Hz or faster. You can set the high-pass filter cutoff around
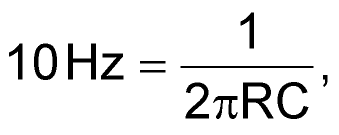
where R is the Thevenin combination of R1 and R2. In the dark detection example, R is 79 kΩ, which yields C = 0.2 µF.
The final circuit now produces a signal that swings from 4 V for a light object (or the light background) to 1 V for a dark object (assuming the contrast ratio is at least 4:1) and can function equally well in a dimly lighted room, normal office lightning, or direct sunlight, just like the human eye.
