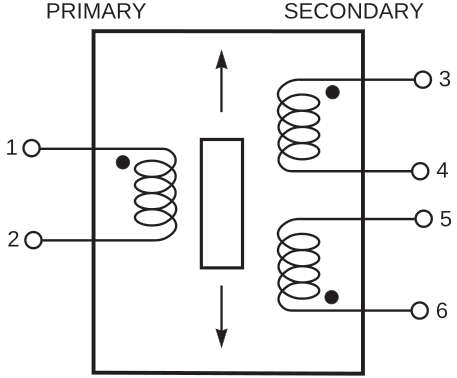
LVDTs (linear variable differential transformers) are electromechanical measuring devices that convert the position of a magnetic core into electrical signals. You generate these signals via excitation on the primary side. The results on the secondary side – typically, two secondary windings – depend on the position of the core (Figure 1).
 |
|
| Figure 1. | An LVDT is an electromechanical measuring device that converts the position of a magnetic core into electrical signals. |
The excitation typically ranges in amplitude from 1 to 10 V and in frequency from 1 to 10 kHz, depending on the type of LVDT you employ. Traditionally, for one circuit to provide such variability in frequency and amplitude, you can use either an LC tank with adjustable components or a sine-wave generator under microcontroller control. It can be difficult to achieve precision over time and temperature with the LC-tank circuit because of variations in passive components. You also must manually perform calibration. You can more easily obtain precision over time and temperature through the use of a microcontroller-controlled sine-wave-generator chip, and calibration can be automatic, but the method incurs a greater expense than the LC-tank circuit. The circuit in Figure 2 presents an alternative.
 |
|
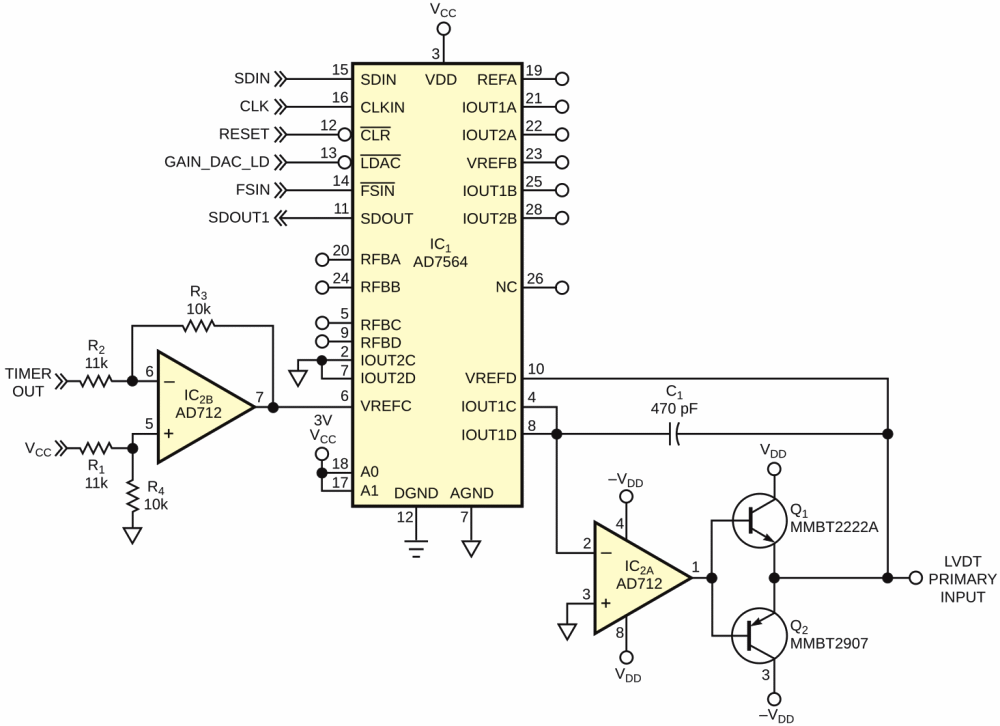
| Figure 2. | This circuit uses a triangular wave from a DAC to excite an LVDT. |
Rather than using a sinusoidal signal to excite the LVDT, a triangular wave comes from the integration of a square-wave output provided by a microcontroller timer. With the use of a current-output DAC, such as the AD7564, you can create a circuit that provides an alternative at a lower cost than that of a sine-wave-generator chip and with greater ease of modification than with an LC-tank circuit. Beginning with the microcontroller, the frequency of the excitation wave depends on the configuration of the microcontroller's timer. You can configure a free-running timer, for example, to toggle the output based on the comparison match of a preset count. You base the count on the desired frequency output and the timer's internal clock rate. You then adjust the output of the microcontroller's timer to remove offset. You need to eliminate as much offset in the signal as possible because such offset adversely affects the transformation process. You can use an op amp to remove the offset because the offset is constant – in this case, half the voltage that powers the microcontroller. In general, you should choose an op amp with low offset and low bias, not only for the difference stage, but also later.
Once you center it about common, the signal becomes a triangular wave. The integrator you use is basically a single-pole, lowpass filter with a configurable (via the DAC) corner frequency. The corner frequency you choose guarantees that integration of the excitation signal occurs. To accommodate variability in frequency and amplitude, the DAC provides an easy interface. With two channels of the AD7564, the circuit can emulate variable resistors for the feed-forward and the feedback of the integrating op amp. (The other two channels could serve for the demodulation gain of each LVDT secondary.) You can use these “resistors” to form the corner frequency for the “lossy” integrator and to establish the gain through the circuit, ensuring that the signal is integrated and that the amplitude of the excitation signal is appropriate for the LVDT.
You need to make several calculations in advance to determine the configuration of the DAC and the establishment of the resistances. According to the data sheet, the resistance of the R-2R ladder in the AD7564 DAC is typically 9.5 kΩ. You can calculate the feedback resistance using the following formula:
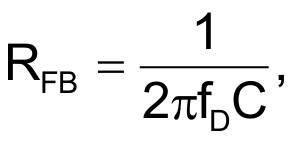
where fD is the desired corner frequency of the integrator and C is the value of the capacitor you use. You can then assemble the data word for that effective resistance accordingly:
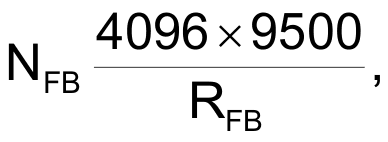
where NFB is the digital word loaded into the DAC. The feed-forward resistance of the integrator circuit is then
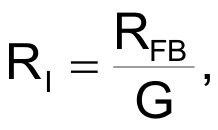
where the gain factor, G, depends on the desired output amplitude. The data word for that effective resistance becomes
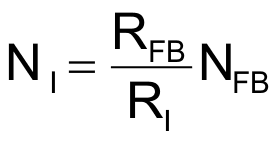
or
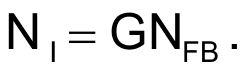
In most cases, you may need to use additional drive current from the output of the “lossy” integrator to drive the primary coil of the LVDT. This approach may entail the addition of transistors and other components.
 |
|
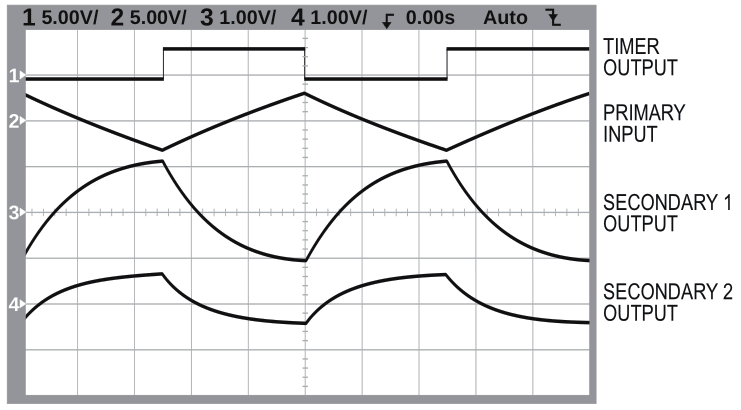
| Figure 3. | Although what appears on the secondary side differs from the excitation signal, it is sufficient because of the inherent filtering properties of the LVDT. |
You have some flexibility in the type of excitation signal the circuit uses because it is common practice to calibrate an LVDT. Figure 3 illustrates the output of the excitation circuit and the results on the secondary side of the LVDT. Although what appears on the secondary side differs from the excitation signal, it is sufficient because of the inherent filtering properties of the LVDT. The output of each secondary side generally transforms into a constant root-mean-square or mean-absolute-deviation value. In the situation of two secondary coils, a comparison between those values occurs. As long as you excite both coils in the same manner – which is guaranteed because only one primary coil exists – and the output signal is of sufficient resolution, then a triangular wave can excite such an LVDT.
