I was surprised recently when a (nearly) two-decade-old design idea of mine for take-back-half temperature control (Ref. 1) got a question from reader John Louis Waugaman. John says he needs a way to control the temperature of batches of rising bread dough. I’m glad he might be considering applying my TBH circuit to his problem, but it really is kind of overkill in that context. So, I began pondering whether a simpler topology might solve his dough incubation problem as well as the TBH circuit would while saving some cost and effort. Plus, there’s a backstory.
For a long while I’ve been fond of a particularly elegant, accurate, and (very!) inexpensive method (∆VBE) for sensing and controlling temperature using ordinary, uncalibrated bipolar transistors. I first saw it explained in an application note (Ref. 2) by famed analog guru Jim Williams (see page 7 for ∆VBE theory).
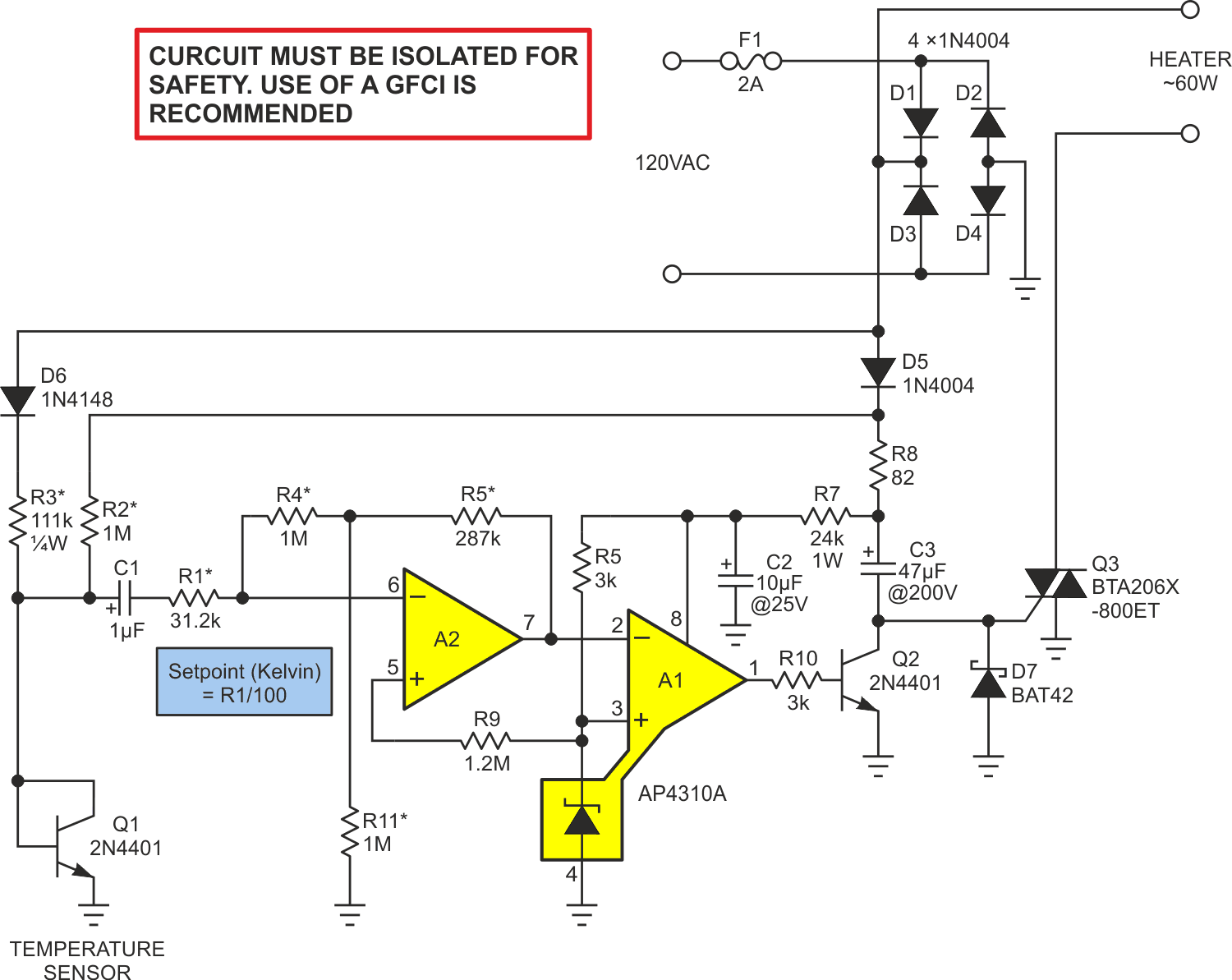
I’m always watching for opportunities to use ∆VBE and this possibility of providing cheap, accurate, and calibration-free temperature control in a cool culinary context was too good to let pass by. Figure 1 shows the new circuit I cooked up, (loosely) based on Jim’s recipe.
 |
|
| Figure 1. | ∆VBE sensor Q1 is programmed via R1 for desired setpoint temperature in Kelvin = R1/100 = 312 °K = 39 °C for R1 = 31.2k. Asterisked Rs should be precision types (1% or better). |
The R2 R3 D5 D6 network drives Q1 in the magic 10:1 current ratio ∆VBE measurement cycle described by Williams. Note that the absolute currents supplied to Q1 are no more accurate than the raw unregulated 60-Hz line voltage that creates them, but that doesn’t affect ∆VBE accuracy. All that counts is their 10:1 ratio which is set independent of line voltage variation solely by the precision of (R2/R3 + 1) = 10.
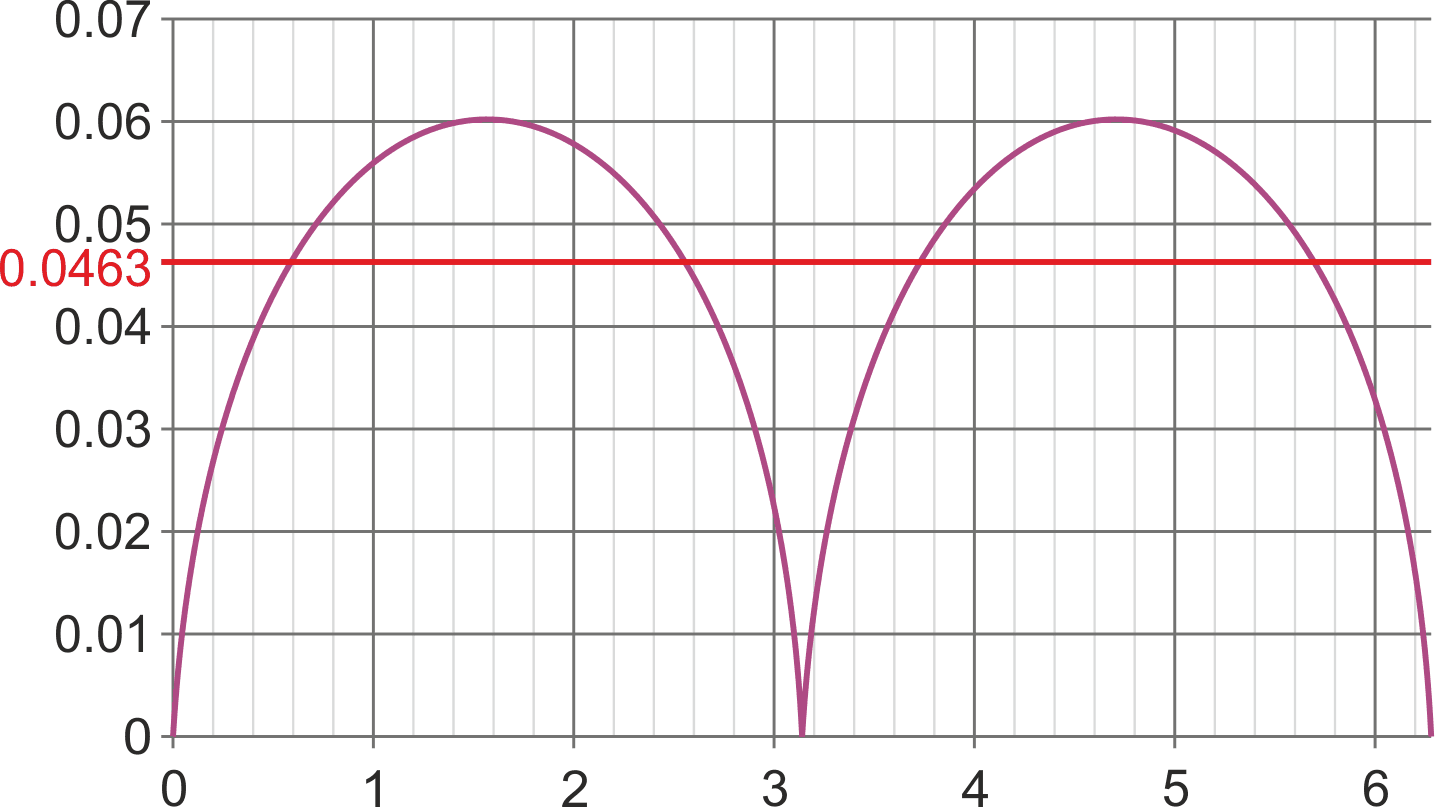
This makes Q1 generate a PTAT (proportional to absolute temperature) AC signal equal to °K/5050 volts peak-to-peak that follows the 120-Hz log(|sine|) waveshape shown in Figure 2.
 |
|
| Figure 2. | Q1’s ∆VBE PTAT log(|sin(r)|) °K/5050 waveform. (Yaxis = volts, Xaxis = radians Red = average value = AC baseline). |
The PTAT signal Vpp is boosted by A1a’s gain = –2,742,160/R1, then compared by A2 to its precision (2.50 V ±0.4%) internal shunt reference (thanks again, Konstantin Kim, for finding the versatile AP4310A!).
A2’s output stays at zero, holding Q2 off, while Q1’s temperature and the PTAT signal are below setpoint. This allows 120-Hz pulses coupled through C3 to reach Q3’s gate, switch it on, and apply power to the heater. When the heater warms Q1 (and presumably the dough) to the programmed temperature, then the PTAT waveform rises above A2’s reference voltage. This makes A2 start turning Q2 on which diverts the TRIAC gate pulses to ground. That turns Q3 and the heater off allowing Q1 to cool, etc., etc. The resulting cycling completes a thermostasis feedback loop to make the dough grow.
About Q3: Even though heater drive is unipolar, I selected a TRIAC instead of an SCR for Q3. This wasn’t to get bipolar capability but rather because the TRIAC has a higher max gate current rating. This makes Q3 able to shrug off the 2-A inrush possible at power-up, which might vaporize an SCR gate.
D7 provides a path to ground for C3 return current, preventing it from false triggering Q3.
For heater duty, John suggested an incandescent light bulb. I agree radiant heating should work well. Since Q3’s maximum duty factor is 50%, a 100-W bulb would be just about perfect for a maximum heating power of ~60 W. Plus, a bonus benefit of reduced voltage would be a lower filament temperature. This should make an ordinary tungsten bulb last many thousands of hours.
It may be just what John kneads.
References
- Woodward, Stephen. "Temperature controller has “take-back-half” convergence algorithm."
- Williams, Jim Williams. Measurement and Control Circuit Collection. Application Note 45.