To measure high levels of direct current for overload detection and protection, designers frequently use either a current-shunt resistor or a toroidal core and Hall-effect magnetic-field sensor. Both methods suffer from drawbacks. For example, measuring 20 A with a 10-mΩ resistor dissipates 4 W of power as waste heat. The Hall-effect sensor delivers accurate measurements and wastes little power, but it’s an expensive approach to simple current monitoring.
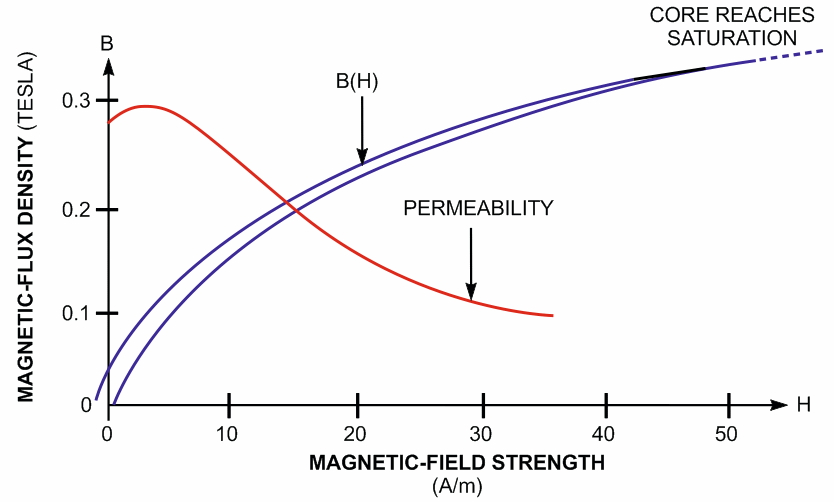
This Design Idea describes an inexpensive, low-power current-measurement circuit that’s useful for measurements of modest accuracy. As a bonus, a filter inductor in a dc/dc converter’s input line can double as a current sensor for the measurement circuit. A representative ferrite core’s permeability decreases as the core nears saturation (Figure 1). The curve’s shape and values depend on the core material’s characteristics and whether the core includes an air gap.
 |
|
| Figure 1. | This representative magnetization (BH) curve shows that, as current through an inductor’s winding increases, so does magnetizing-field strength, H. When magnetic-flux density, B, can no longer increase, the core’s magnetic material has reached saturation. |
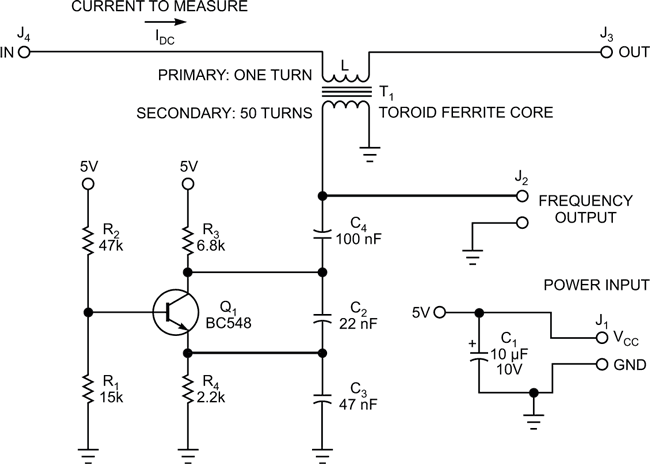
The core’s permeability depends on the magnetic-flux level in the ferrite material, which in turn depends on the amount of current flowing through the core’s windings. This circuit uses a simple LC oscillator to measure the core’s permeability. A primary winding comprising one or more turns wound on the core carries the measurement current. A multiturn secondary winding on the core forms an inductor, L, that determines the oscillator’s resonant frequency.
 |
|
| Figure 2. | Varying the direct current flowing through the single-turn primary winding alters T1’s secondary winding’s inductance, which in turn varies the oscillator’s output frequency. |
In theory, any LC oscillator circuit will serve in this application, but, in practice, the current-measurement winding presents low impedance that damps the LC-tank circuit and causes start-up and stability problems in some oscillator circuits. Of a variety of tested oscillator circuits, the design in Figure 2 offers the best performance. A number of factors affect the core’s permeability, which in turn impacts the circuit’s frequency stability and limits its applications to current-overload detection and low-accuracy current measurements.
 |
|
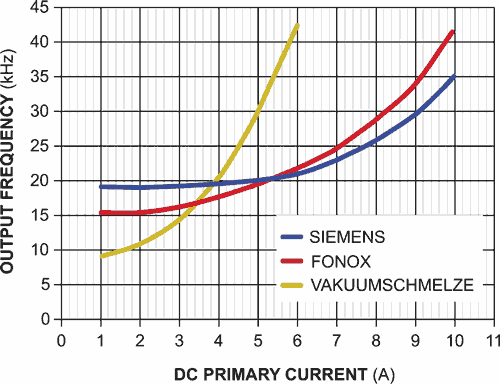
| Figure 3. | Current-versus-output-frequency plots for three manufacturers’ toroidal cores show the influence of the cores’ characteristics on frequency linearity and relative sensitivity. |
Figure 3 illustrates the circuit’s output-frequency-versus-current characteristics for three vendors’ ferrite cores of identical dimensions and number of secondary turns. For best linearity, use a low-hysteresis core material. Cores of virtually any dimensions and materials work in the circuit but require optimization of the number of turns on the oscillator tank and primary windings. Increase the core’s air gap, if present, when the current you apply to the core causes saturation before reaching the overload value. For improved performance and linear measurements, use the circuit in a closed-loop configuration (Reference 1).
Reference
- Nell, Susanne, “Improved current monitor delivers proportional-voltage output”, EDN, Jan 19, 2006, pg 84.
