Les Hughson
EDN
The ATMega168 is a great general purpose 8-bit AVR microcontroller from Atmel. It has 23 GPIO pins, but sometimes (as I have found) you can run out of I/O pins as your design grows. This happened to me recently when, of the 23 GPIO pins available, 2 were taken up by an external ceramic resonator, 1 for the reset line, 3 for serial coms, 14 for the LCD, and 3 for RGB LED control. This used all 23 GPIO pins, with none left for the four buttons I needed. What to do? This Design Idea has the solution.
A close look at the ATMega168 data sheet revealed that the I/O pins available on the 28-pin DIP package and on the 32-pin TQFP package are not all the same. On the TQFP package, there are an additional pair of VCC & GND pins and an additional two ADC input pins on top of the advertised 23 GPIOs. So if I could read my 4 buttons with these extra ADC inputs, all would be OK and the design would be saved.
Now, the user interface was fairly overloaded with functions, and various combination button pushes were used to call up different menus on the LCD. Also, the software was still under development and more combination button pushes might be called for. I wanted to be able to detect each button individually as well as all possible button push combinations, so for four buttons, I needed to detect a total of 24, or 16 possible button states.
OK I thought that should not be hard. I just need a resistor network between my four buttons and one of the ADC inputs so each button pulls down a different amount and all 16 combinations are evenly spaced between VCC and GND (Figure 1). However when I tried to do this it turned out not to be as easy as it looked at first sight.
 |
|
| Figure 1. | Four-button resistor network. |
I considered using an R2R resistor ladder, but this requires SPDT buttons so the inputs are connected to VCC or GND, not left floating. After thinking about this for a while, I realised I was making things more difficult for myself than I needed to. There are two ADC inputs available, so if I put only two buttons on each input, then each would only need to detect 22, or 4 possible button state combinations instead of 16 (Figure 2). If the states are not evenly distributed between VCC and GND, it would not matter too much.
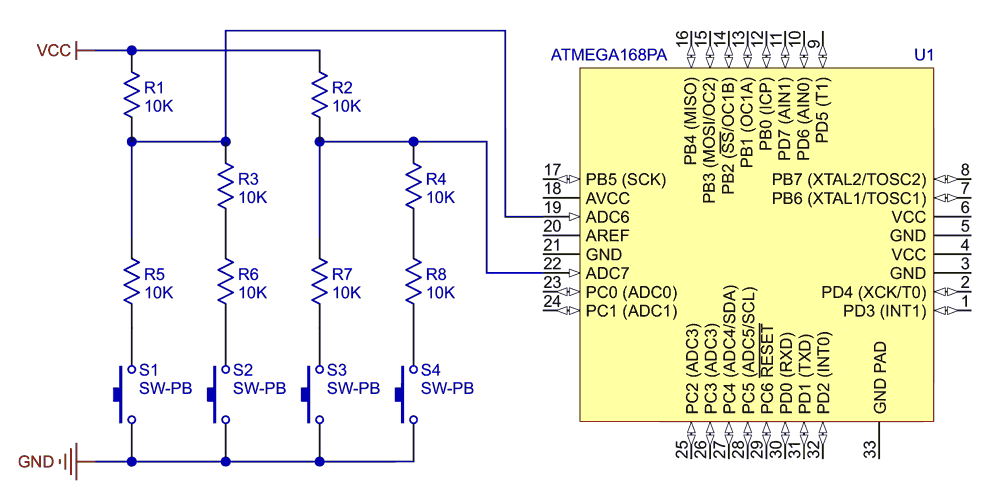
This resulted in the circuit of Figure 3, which proved a successful solution and has now been in production in my client’s product for some time. The resistors are all the same value, so a four-resistor network like this Bourns 1206 part can be used for a small, neat solution.
 |
|
| Figure 2. | Simpler two-button resistor network. |
The spreadsheet in Table 1 details the operation of each circuit (download the design files at the end of the article). The yellow cells are where you enter the resistor values used, the supply voltage, and the ADC resolution. The green cells are calculated outputs showing the operation of the circuit. The first three columns show a truth table of the button inputs, and the R Buttons column shows the total pull-down resistance resulting from the different button combinations. The Vout and Counts columns show the voltage input to the ADC and the resulting ADC reading. Count Mid Points shows values midway between the expected ADC values – it is these that are used to differentiate the different inputs and decode the button pushes. This ensures that all possible input values are decoded and maximum allowance is made for variation due to resistor tolerance, noise, etc.
 |
|
| Figure 3. | Partial schematic showing two two-button circuits. |
The software decodes which combination of the four buttons is pushed, debounces the button inputs, and handles button repeat operations when certain buttons are held down.
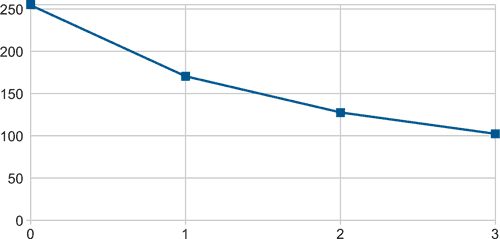
As can be seen, the code distribution is not at all linear. However, even the closest values still maintain a reasonable separation for practical operation. A graph of the results (Figure 4) shows the nonlinearity and also highlights that almost half the ADC input range is unused by this circuit.
 |
|
| Figure 4. | Button states vs. values. |
This is a reasonable trade-off for simplicity, but it made me wonder if I could do better, and brought me back to reconsider the initial idea of Figure 1. It seems logical to expand the two buttons to four by extending the resistor value progression from 10K, 20K to 10K, 20K, 40K, 80K. However, this does not address the nonlinearity problem or the wasted ADC range.
An improved approach would be to replace the pull-up resistor (R1 in Figure 3) with a constant current source. Then, the button resistor network will convert the constant current into a nice, evenly stepped output voltage. This could probably be done using a voltage reference (e.g., TL431) and a transistor. But that means additional active components and careful design. This is getting away from the initial vision of a simple resistor network.
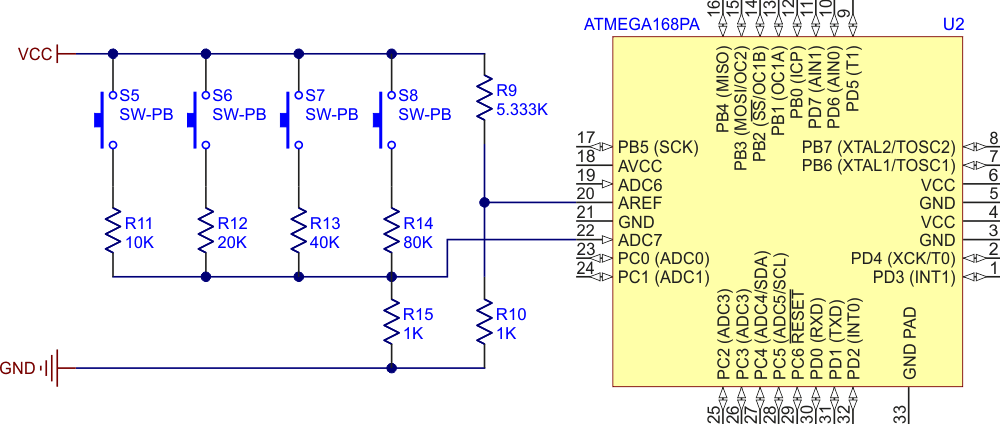
Another approach would be to treat the four-button resistor network as if it were a variable-resistance sensor, like a thermistor, and use the same methods used to read those. This lead to the idea of putting the button network in a bridge circuit. This also matches the signal spread to the ADC input range. With careful resistor selection, it is also possible to improve the nonlinearity. After some experimentation, this lead to the circuit in Figure 5.
 |
|
| Figure 5. | Four-button circuit. |
This circuit uses only one ADC input for the four buttons, leaving the other ADC input for more buttons or other uses. The four buttons and series resistors form one side of the bridge, and R9/R10 forms the other leg. This is used as the reference voltage for the ADC – equal to the ADC’s maximum input voltage. The resistor values are selected so that R10 = R15 and R9 equals the parallel combination of R11 to R14, thus allowing full use of the ADC input range. Keeping R15 and R10 small improves the linearity of the result at the expense of reducing the actual voltage swing.
Note that these resistor values are not easy to get in practice, but they can be made using standard values in combination: series-connected 20K resistors for R13/R14, and two parallel 10K parts in series with three parallel 1K resistors, to make R9. By using these three values, four resistor networks and one resistor will complete the circuit.
The graph of Figure 6 illustrate the circuit results, which show a much more linear operation than before. This circuit could be extended to five or perhaps six buttons by continuing the geometric resistance sequence. However, care must be taken that the resistor values are accurate enough to ensure reliable operation, and some experimenting with the spreadsheet and min/max resistor values would be needed to check this.
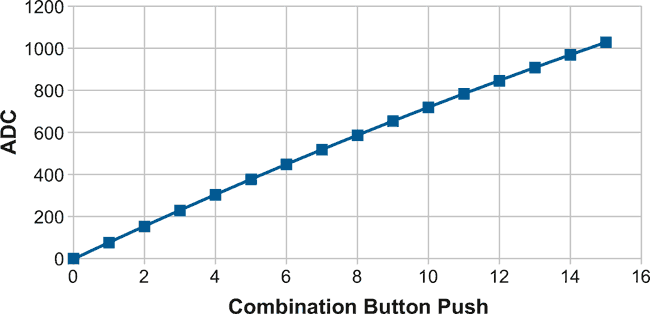 |
|
| Figure 6. | Button states vs. values. |
Experience from building and testing this circuit exposed a small problem in that the AREF pin of the microcontroller draws a small current which introduces an error into the AREF voltage. This current is graphed in the microcontroller datasheet and seems to be well defined. To correct for this, a 33 Ω resistor can be placed in series with R10. With this correction, experimental results produced 8-bit ADC readings within one count of the spreadsheet-predicted values. The software for this version is left as an exercise for the reader.
 |
|
| Figure 7. | Four-switch prototype. |
It is also possible to do without R9 and R10 by using the microcontroller’s internal 1.1 V reference. In that case, change R15 from 1K to 1.5 K. However, the accuracy of VCC will then affect the readings.
So, after a lot of work, it seems the initial goal from Figure 1 was not too hard after all.
