Op-amp integrators can ramp to saturation, and a capacitor-discharge switch can reset them. Alternatively, you can input-switch them to ramp up and down in triangle-waveform-generator applications. Much searching through online “cookbook” circuits turned up no means of ramping an op-amp integrator to hold at a preset constant voltage level. This Design Idea describes a single-supply op-amp circuit that outputs a rising or falling linear-voltage ramp in response to a step change of a positive dc-input voltage of 0 V to VCC. The output ramp’s dV/dt slope is adjustable to 1 V/minute with the values in Figure 1, is independent of the input-step amplitude, and terminates at a constant dc level approximately equal to the input-step voltage. Any further change in the dc-input voltage causes the output to ramp up or down at the preset dV/dt to the new dc-input voltage. In effect, this circuit is an amplitude-bounded constant-slope integrator.
 |
||
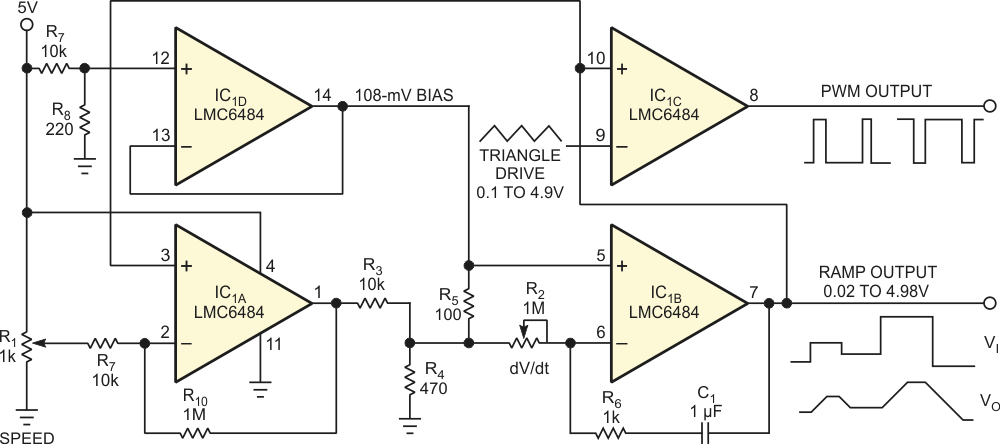
| Figure 1. | This op-amp integrator ramps up or down at a preset rate, holding a final value equal to the input-voltage dc level. |
|
The circuit uses a rail-to-rail I/O quad op amp, the Texas Instruments LMC6484. The rail-to-rail feature makes it easy to use, the low input leakage is great for long-time-constant integration, and the 3-mV maximum input-offset voltage is respectable. Potentiometer R1, a linear taper, sets the input voltage for final output voltage after the ramp ends. IC1A’s output is in saturation at VCC or ground while the output is ramping down or up, respectively.
Nonpolarized capacitor C1 and potentiometer R2, a linear taper, determine the time constant of integrator IC1B. The adjustment range is 0.5 V/msec to 1 V/minute. The reference bias for IC1B is 108 mV, which you derive from IC1D as a unity-gain buffer for divider R7 and R8. R6 ensures that you do not exceed IC1B’s input current when you turn off the power, that C1 discharges through IC1B’s input and output diodes, and that IC1B’s output does not excessively load back into IC1D’s output with R2 at a minimum.
R3 and R4 divide the saturated IC1A’s output to approximately 100 mV unloaded above or below the 108-mV bias. This division causes approximately 20 mV to drop across R5 to slew IC1B upward or downward at the integration rate that C1 and R2 set; 20 mV is comfortably above the op amp’s possible 3-mV input-offset voltage to minimize offset effects. When IC1B’s output-voltage ramp reaches that of the input voltage from the R1 wiper, IC1A comes out of saturation and rests at approximately 2.5 V, providing the loop-negative feedback to maintain integrator IC1B’s output equal to the input voltage. This action sets the boundary on the integration ramp’s terminal voltage. IC1C can be spare, or, as the Figure 1 shows, you can drive it with a triangle-wave signal to convert IC1B’s dc level or ramp to a corresponding PWM (pulse-width-modulated) signal for a motor-drive circuit (not shown).
R5 eliminates differential errors arising from bias-resistor tolerance, and it provides a compromise between IC1B’s 3 mV maximum input-offset voltage at 25 °C and 20-mV input amplitude to allow the slowest dV/dt. The values in the Figure 1 result in a maximum time of approximately 1 V/minute, or 5 minutes at VCC of 5 V to reach full speed. If you require longer times, you can raise VCC to 15 V with adjustments to the bias resistors or raise C1’s value by using parallel nonpolarized capacitors. Alternatively, you could raise R2’s value, although selection is sparser for potentiometers with values greater than 1 MΩ.
If your application does not require a long time constant or if you use the aforementioned methods to increase the time constant, you can eliminate R5 at the expense of a higher level differential input to IC1B and correspondingly faster integration. You could also eliminate IC1D and the R7-R8 resistive-bias divider that connects directly to IC1B’s Pin 5, but resistor tolerance becomes more critical to minimize differential error (reference 1 and reference 2).
References
- “Tractive effort, acceleration, and braking,” The Mathematical Association, 2004.
- Woof, Tony, “Kilo newtons, kilo watts, kilometres per hour,” 2001.
