Among the methods available for airflow measurement, thermal flow meters enjoy the virtues of simplicity. They also offer simple construction, low cost, and superior sensitivity to low flow rates (less than 1000 fpm). All thermal anemometers make use of the relationship between airspeed (AF) and the thermal impedance (ZT) of a heated sensor. One practical example of such a relationship is this model of the TO-92's thermal impedance:
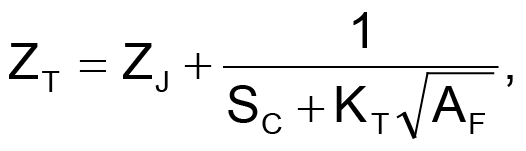
where:
ZJ = "total immersion" junction-to-case thermal impedance = 44 °C/W,
SC = still-air case-to-ambient conductivity = 6.4 mW/°C,
KT = King's Law thermal diffusion constant = 75 µW/°C·√fpm,
AF = airspeed in ft/min.
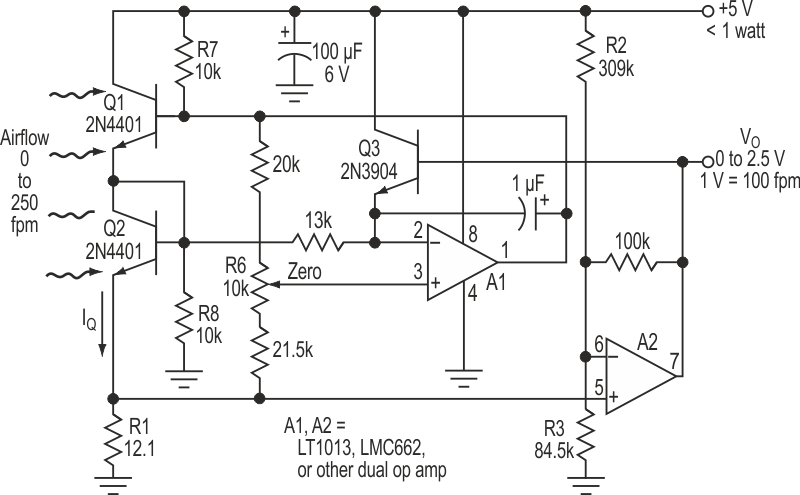
In this model, the raw sensor output is inherently nonlinear with airspeed, a problem common to all thermal airspeed sensors. To compensate, thermal anemometer designs must include some provision for measurement linearization. The circuit in Figure 1 combines ideas from two earlier IFDs (Ref. 1 and Ref. 2). In doing so, it implements a simple, linearized (±5%), ambient-temperature-compensated thermal anemometer. A robust, power-efficient device, it draws less than 1 W of total operating power from a single regulated 5-V rail.
 |
|
| Figure 1. | The circuit combines ideas from two earlier IFDs to implement a simple, linearized thermal anemometer. An ambient-temperature-compensated device, it is robust and power-efficient. |
In operation, A1 maintains a constant temperature differential (about 25 °C) between Q1 and Q2, independent of changes in thermal impedance and ambient temperature. A1 achieves this by maintaining a constant ratio between the two transistors' VBE voltages. It can do so by controlling the collector currents of the series-connected devices, and thereby their power dissipation.
Since both transistors pass the same current (IQ), their relative power dissipations are determined solely by their respective VCE voltages. VQ1 > VQ2 for all valid operating modes (Q3 sees to this). So for any given IQ, Q1 will always dissipate more power and more heat, meaning it will run hotter than diode-connected Q2. Consequently, as airflow increases and thermal impedance decreases, A1 can hold any chosen Q1/Q2 temperature differential by increasing IQ. The resulting airflow-dependent IQ is sensed by R1, then offset and boosted by A2. In turn, it becomes the 0- to 2.5-V anemometer output signal VO, scaled for 10 mV = 1 fpm = 0 to 250 fpm (~2.5 kts).
Meanwhile, Q3 acts with A2 to limit the maximum voltage across R1 to about 2 V. This is done to avoid the risk of latch-up, which would occur if A1's output were allowed to rise too near the 5-V rail. In that event, VQ1 would approach VQ2. As a result, it would be impossible to achieve the programmed temperature differential and Q1/Q2 VBE ratio, no matter how high IQ might rise. Similarly, R7 and R8 prevent latch-up when the circuit is first powered up.
 |
|
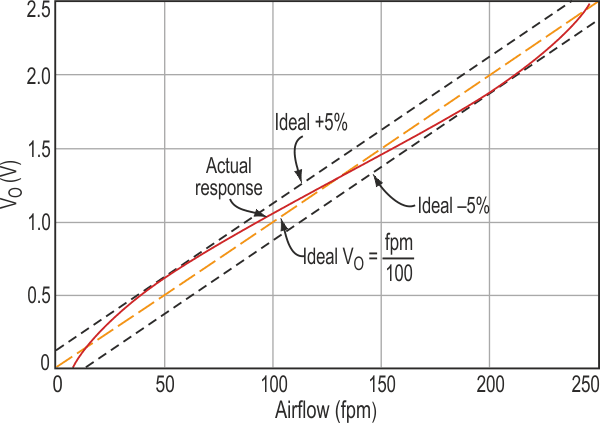
| Figure 2. | The quadratic relationship between IQ and Q1/Q2’s power dissipation does a fair job of canceling nonlinearity, erasing all but ±5% FSR linearity error over the range of on-scale airspeeds. |
But what about measurement linearization? As illustrated in Figure 2, the inherent quadratic relationship that exists between IQ and Q1/Q2's power dissipation does a fair job of canceling nonlinearity. It erases all but ±5% FSR linearity error over the entire range of on-scale airspeeds. Also, anemometer calibration is quick and straightforward. The transistor sensor pair is simply placed in slowly moving air (almost, but not quite stagnant; AF = 5 to 7 fpm is ideal). R6 is then adjusted for VO = 0.
The "tranemometer" is illustrated with circuit constants that scale its output for VO = 0.01 V/fpm = 1 V/ kts. Yet virtually any range of airflow rates can be accommodated with appropriate choices for R1, R2, and R3.
References
- "Low-Power Thermal Airspeed Sensor," Electronic Design, May 25, 1998, p. 116.
- "Low-Power Solid-State Airflow Detector," Electronic Design, Jan. 22, 2001, p. 118.
