Earplugs ready? Let's make some noise!

Microchip PIC12F1501 MCP6002 MCP6004 MCP6022

Usually, noise annoys. Occasionally, it can be a valuable tool. Surprisingly, there is a whole palette of noise colors [1]. This design idea (DI) shows good ways of generating the commonest and most useful ones, which are white [2] and pink [3] and optionally brown [4]. At its heart is a microcontroller programmed to generate raw white noise and a much-improved filter to convert that into pink.

Sources of random electronic noise are all too common. The most controllable source of the white stuff is probably the well-known pseudo-random binary sequence [5] (PBRS) generated by a shift register with feedback, and that will be our starting-point. A fairly standard implementation using logic ICs is shown in Figure 1.


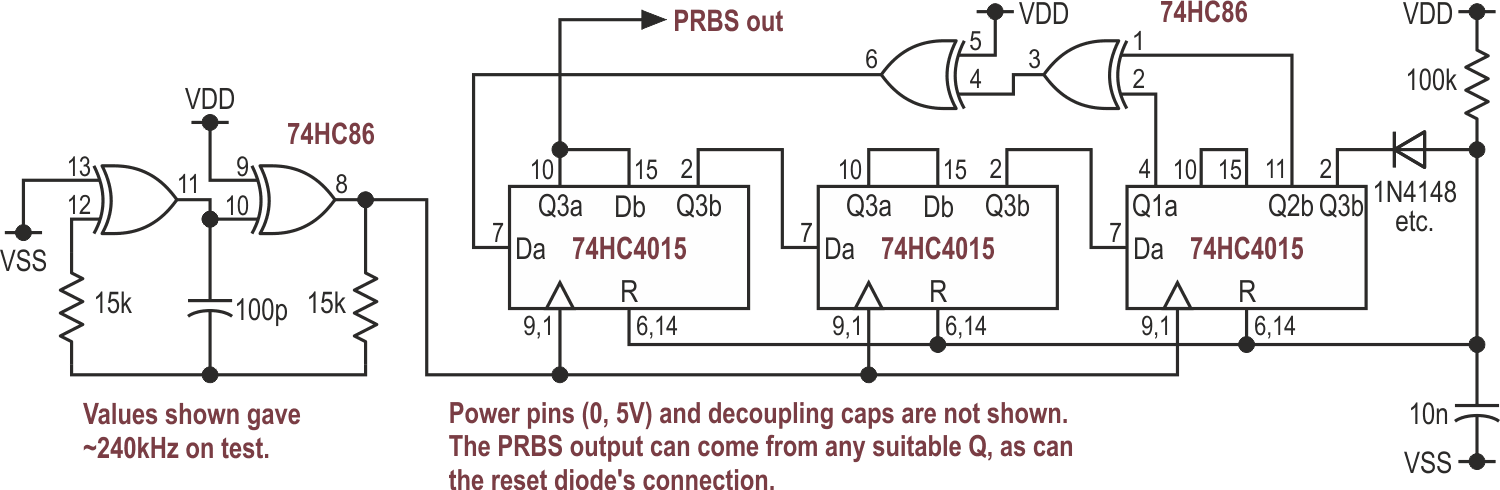Figure 1.	*A pseudo-random sequence generator (PRSG) built with standard logic ICs generates wideband white noise.*

Three 8-bit devices (or dual 4-bit ones, as here) are concatenated to make a 23-bit shift register. The outputs from bits 18 and 23 are EXORed and inverted (or EXNORed) and fed back to the input, producing a pattern of bits which appears random though it repeats every 2²³–1 clock cycles, which at a clock rate of 240 kHz is about every 35 seconds. (That “–1” represents the illegal, locked-up, all-1s condition, against which the simple reset circuitry guards.) For frequencies up to about a tenth of the clock rate, the spectrum is virtually identical to that of pure and ideal white noise. It has the same intensity in any given bandwidth: its spectrum is flat. For other colors, we just need to filter it appropriately.

A cheap microcontroller makes a good PRSG

So far, so conventional. But why use 62-pins-worth of chippery plus at least ten discretes when a single package with 8 pins – or even fewer – will suffice? The schematic for that is too boring to show – imagine a rectangle fed with power (decoupled with a single cap) and having a GPIO pin delivering the PRBS – but here is the MPASM assembly-language code [6] for doing it with on a Microchip 12F1501 PIC. (It should open cleanly with Notepad.) The code is logically and functionally identical to Figure 1’s circuit and can easily be modified for use in different low-end PICs, while the underlying logic can be ported to any other suitable µC. (Back in the day, NatSemi made the MM5837, an 8-pin, 15-V, PMOS white noise source using 17 stages. It’s long obsolete, but this could be a nice substitute for it.)

We now have pseudo-random white noise with a spectrum ranging roughly from 30 mHz to a few MHz, which is just a few more octaves than we need. (There are nulls at multiples of the bit rate, which is 267 kHz for this PIC version.) It’s still in the form of a pulse stream, which needs band-limiting before we have truly useful white noise. For pink noise, further filtering is needed so that all octaves (or other frequency ratios) have the same intensity, which is what we need for audio use. The circuitry to do all this is shown in Figure 2.


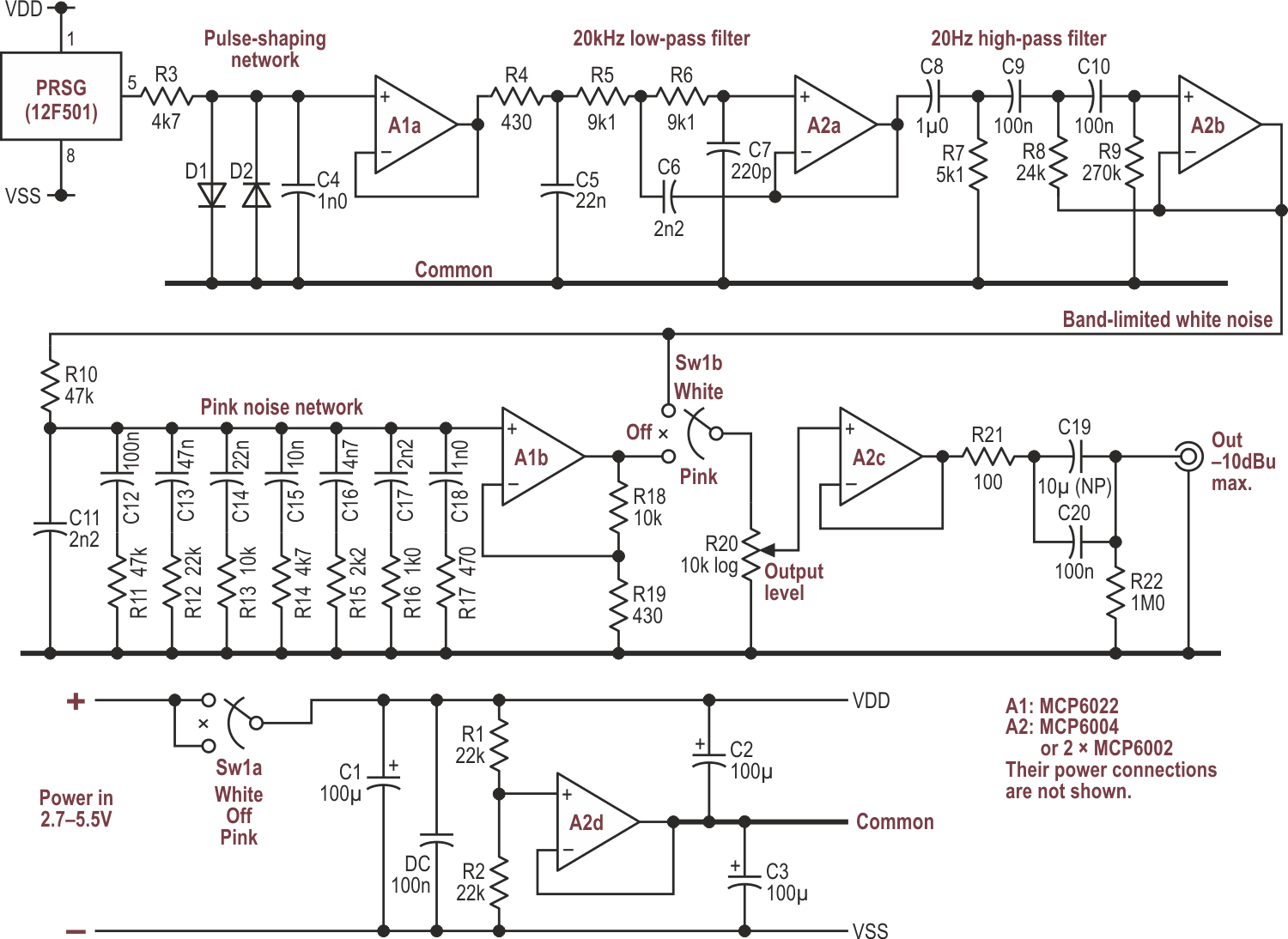Figure 2.	*A pseudo-random signal – white noise – is tailored to fit within the audio band, and further filtered to produce pink noise as well.*

The PRSG could use Figure 1’s discrete logic, but the micro version is electrically quieter (hah!) as well as being more compact and, ignoring programming overheads, cheaper. The pulse-shaping network turns the rail-to-rail rectangular pulse stream into trapezoids having a defined level (about 1.2 V pk-pk) and with slew rates less than those of the downstream op-amps. The 20 kHz low-pass filter does what it says. (That “20 kHz” isn’t its 3-dB corner, but a label for its function.) Only high-pass filtering from ~20 Hz is now needed to give white noise within the audio spectrum and at a level of just greater than –10 dBu.

A new and improved pink noise network

Pink noise is a little trickier and needs a more complex filter to give the necessary 3.01 dB/octave (10 dB/decade) slope. Most published solutions use four RC sections as well as the basic R and C shown in Figure 2 as R10 and C11, with some having even fewer. (And many appear to be clones.) Those RCs have their component values spaced by around √10, but some thought and playing with LTspice showed that far better results come from using a few more stages, and ratios close to the cube root of 10. Figure 3 shows the calculated response of Figure 2’s seven-stage network without the added high- or low-pass filters. Even with E12 component values, it is almost a straight line, unlike the clones’ responses.


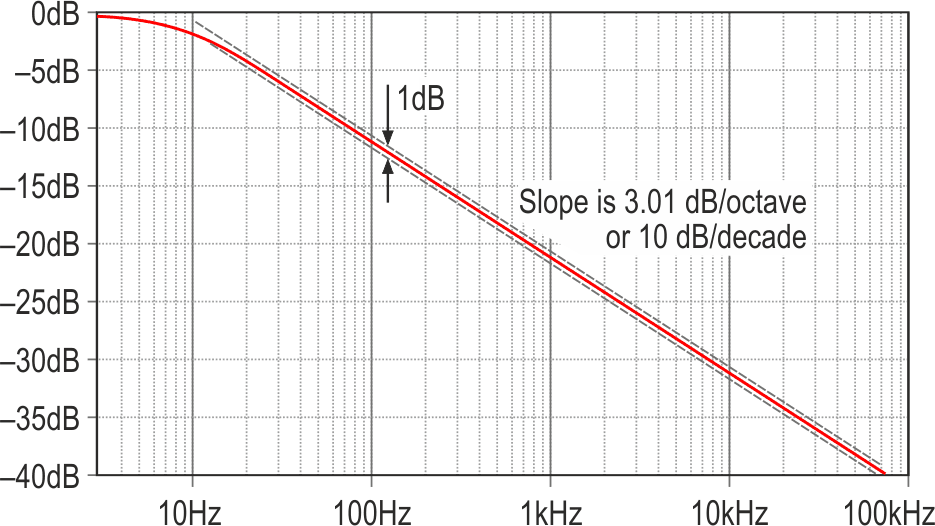Figure 3.	*The response of the new 7-stage pink noise filter, taken in isolation.*

A gain stage brings the pink noise’s RMS level up to –10 dBu to match that of the white, while a selection switch, level-control pot, output buffer, and rail-splitter (A2d etc.) complete the design. Figure 4 shows the calculated response curves along with the worst-case deviations from ideal.


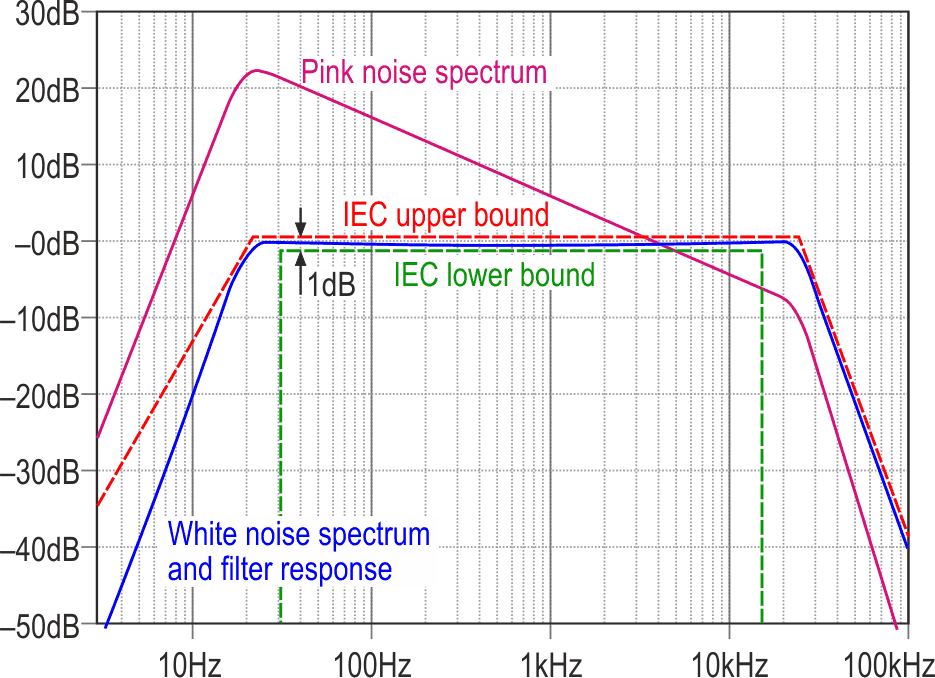Figure 4.	The calculated responses of the completed design, showing the mask for IEC 60268-1 limits and the peak errors of the filters.

The output is now within ±0.2 dB of the ideal from 24 Hz to 21 kHz. With slightly softer HP and LP filters even that could be improved on, especially by reducing the ripple at the ends of the spectrum, but they were calculated to meet the requirements of IEC 60268-1, which refers to the performance, testing, and application of audio systems.

Some further notes on the circuitry

Figure 2’s circuit was designed (and tested) to use a nominal 5 V (or ±2.5 V) rail (what are cheap power banks or surplus USB PSUs for?) but the extremes of 2.7 V (three end-of-life AA cells) and 5.5 V (USB limit) allow for other powering options.

The shaping network ensures that the output will be reasonably constant no matter what the rail voltage may be, and the signal levels of –10 dBu avert clipping even for low rail voltages. With a guaranteed 5 V supply, A2c could have about 7 dBs of extra gain before clipping starts. The output crest factor – the peak-to-RMS ratio – is fairly high, at around 5:1 or 14 dB.

A1a uses the MCP6022 rather than the MCP6004 (or MCP6002s, of course) because the latter can only just cope with the shaped pulses and distorts them noticeably. The gain needed after the pink noise network is rather high, so A1b is also a ’6022: faster, and with lower input offset. The ’6004 works fine in all the other positions. The components between A2c and the output aren’t mandatory, just good practice.

Current consumption was about 6 mA, unloaded.

Brown(ian) noise generation

Adding brown – or red, or Brownian – noise generation is simple, as sketched in Figure 5. All that’s needed is an RC network, giving a 6.02 dB/octave (20 dB/decade) fall-off with increasing frequency, followed by lots of gain. (Some sources specify two cascaded 3 dB/octave – pink – networks, but surely that’s more expensive and less accurate?) The values shown give a –10 dBu output (~2.6 V pk-pk) to match the other responses. Obviously, the switching shown in Figure 2 needs to be changed if you want to add this. For use in isolation, precede it with at least the 20 Hz high-pass filter, or your woofers may try to simulate a small earthquake.


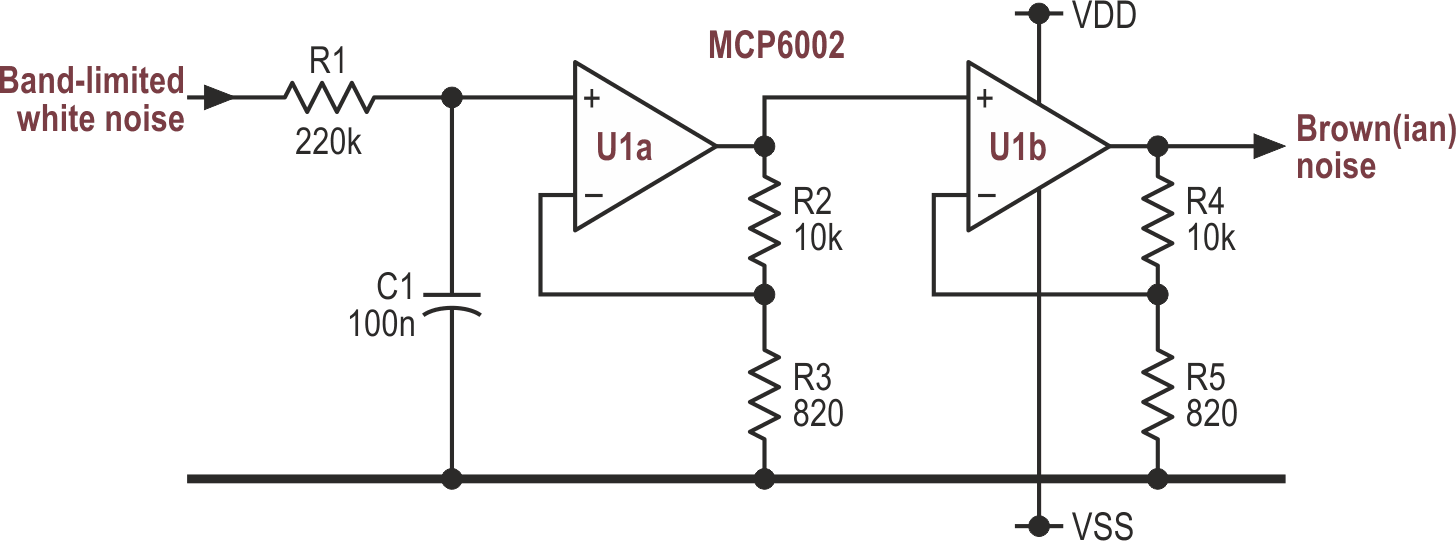Figure 5.	*This simple circuit converts white noise into Brownian.*

Implementing other pseudo-random sequence lengths

The PIC- (or other µC-)based PRSG may have other uses needing different sequence lengths. It’s trivially easy to change the code as long as only two taps from the (virtual) shift register are needed; more taps would need more XNOR code. This reference [7] has a comprehensive table showing the necessary taps as well as a lot of useful background information.

Longer sequences just need extra registers, with each one adding a single processor cycle; the XNOR logic takes longer to run (12 cycles) than the shifting. Eight concatenated registers with feedback from bits 62 and 63 would give a sequence that only repeats after some 1.2 million years, assuming a clock rate of 16 MHz (4 MHz instruction rate). Using 10 registers, tapped at bits 70 and 79, ups that to around 77 billion years. Long enough? If not, the above reference gives many 2-tap solutions for up to 167 bits. You might then want to invest in some ultra-ultra-long-life batteries or a really, really reliable UPS.