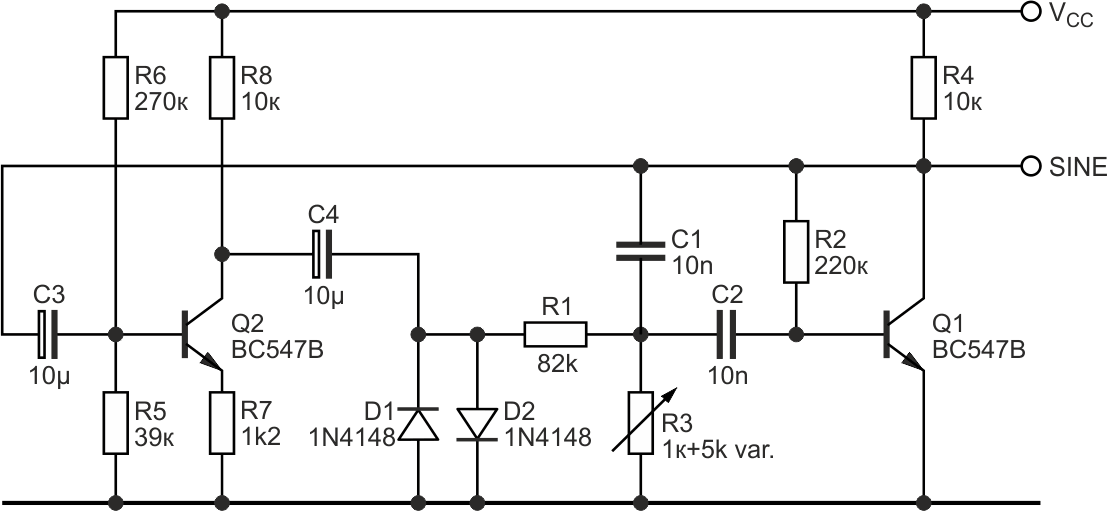
Figure 1 shows a variation on a sine wave oscillator, it uses just two transistors and a single variable resistor to set the frequency.
 |
|
| Figure 1. | Just a couple of components are needed for a simple tunable sine wave oscillator. |
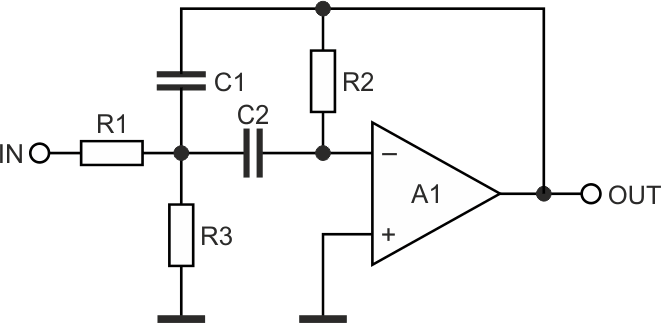
The section around Q1 is a multiple-feedback-bandpass-filter (MFBF). The usual embodiment of this type of filter is shown in Figure 2.
 |
|
| Figure 2. | A standard implementation of a MFBF. |
The formulas for these filter can be found in almost any textbook (where C = C1 = C2):
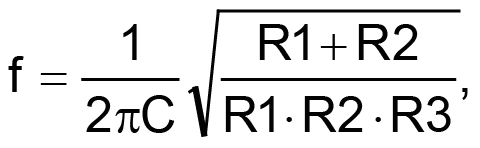
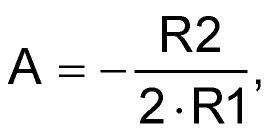
Please note that the center frequency, among others, is determined by the resistance of R3. The gain of the filter is determined by the ratio of R2/R1 in such a way that
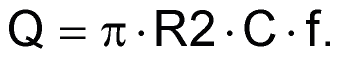
Usually this filter is implemented around an operational amplifier, it can also be implemented around an inverting transistor amplifier. However, because of the limited open-loop gain of the latter, the gain will be lacking at the higher frequencies.
The section around Q2 is an inverting amplifier, with an unloaded gain set by R8/R7. D1 and D2 together with R8 form a clipper to make sure that the signal offered to the MFBF is of constant level.
At the center frequency of the filter, the phase-shift is 180°. Together with the 180° phase shift of Q2 there is a total 360° phase shift at this frequency. The loop gain is >1 due to the ample gain of Q2. Thus, Barkhausen’s criteria are met.
The relative soft clipping of D1 and D2 together with the filtering of Q1 limits the amount of harmonics in the output signal. The passive components around Q1 determine the center frequency.
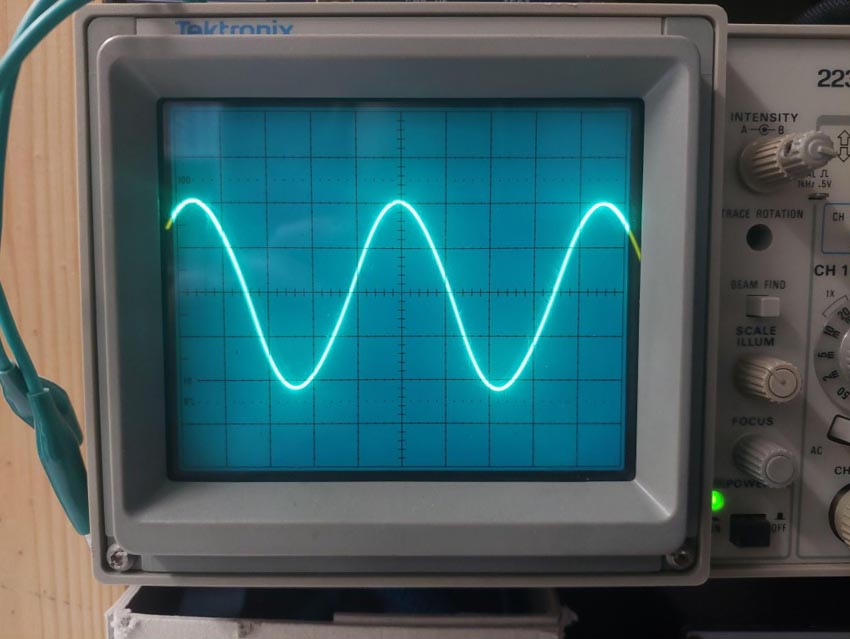
With the current values, the frequency can be set between 498 Hz and 1230 Hz by changing R3 between 1k and 6k. At the same time the output amplitude changes from 1.28 Vpp to 0.68 Vpp. The output shows around ~1% distortion (Figure 3).
 |
|
| Figure 3. | The scope image shows the oscillator output at circa 1 kHz. |
A variation in the supply voltage from 9 V to 12 V causes a frequency variation of only 2 Hz and a variation of output amplitude from 0.80 Vpp to 0.86 Vpp.