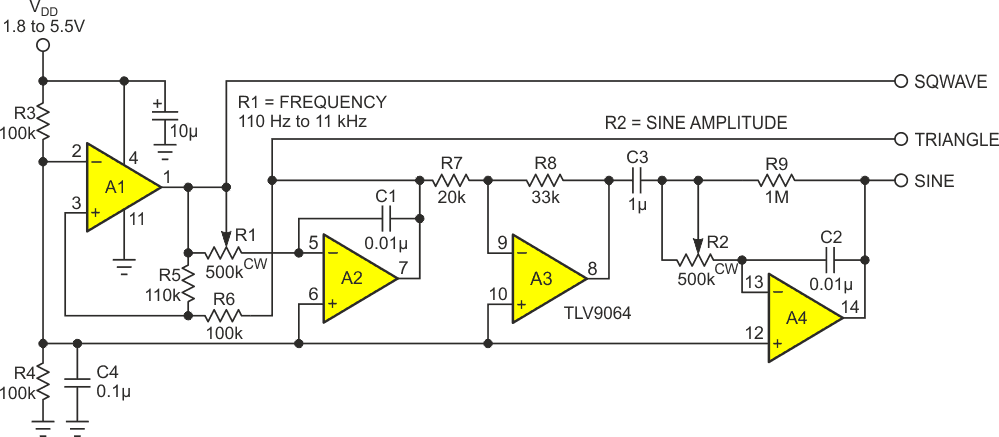
The traditional analog function generator with its customary triple-threat ensemble of square, triangle, and sine waveform outputs is a familiar tool on electronics lab benches. It’s also a classical design exercise. Generally, the square and triangle are easy, so the problem is how to generate an acceptably accurate sine wave. This usually involves some method of conversion of the triangle. Figure 1’s generator circuit employs the popular integrator solution, but with a useful twist.
 |
|
| Figure 1. | Quad highspeed RRIO TLV9064 op-amp performs as comparator, integrator, and clipper while sipping single-digit milliwatts from a single, flexible, power source. |
A1 and A2 combine to form a conventional multivibrator generating symmetrical (around VDD/2) squares and triangles. The peak-to-peak amplitude of the latter is fixed by R5 and R6 at 0.909VDD, and the frequency of both is settable over two decades (and perhaps a bit more) by R1C1.
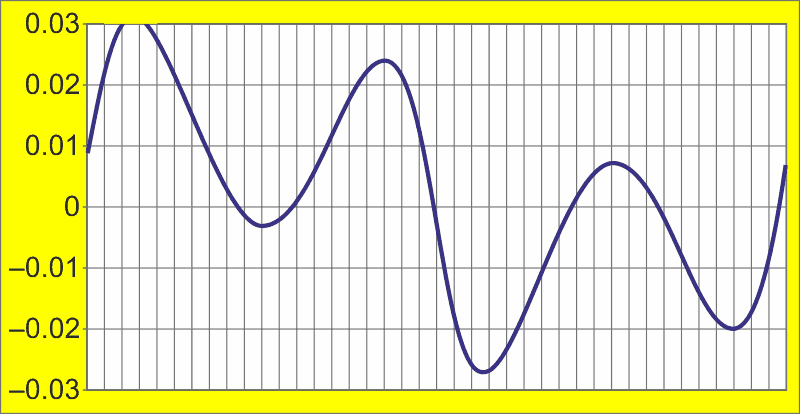
Conversion of A2’s triangles into a (more or less) serviceable approximation of a sine wave could now be, and popularly would be, accomplished by simple integration of A2’s output. But the downside of unadorned integration is found in that ominous phrase “more or less”. Unfortunately, the resulting approximation, while definitely looking a lot like a sinusoid, would quantitatively differ from a true sine function by the ±3% of full-scale, mainly third harmonic, error shown in Figure 2.
 |
|
| Figure 2. | Simple integration of triangle would result in ±3%, 3rd harmonic sine error. |
But maybe we can do better.
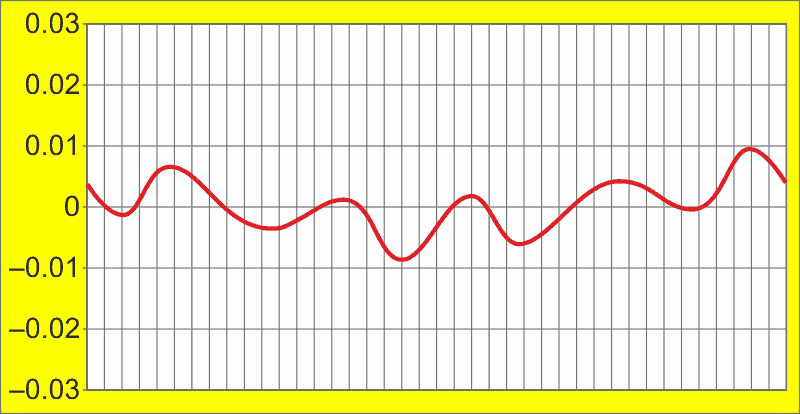
A little experimentation and simulation revealed that simple truncation of the triangle at ±2/3rds of full-scale (VPP = 0.67VDD) prior to integration yields a surprising 3x improvement in sinewave accuracy, shown in Figure 3’s plot of the residue error function.
I say “simple” because we already have an extra amplifier (A3) available. So, it only costs two extra resistors (R7 and R8) to generate the clipped at 67% trapezoidal waveform. This does a better job of approximating the dV/dT of a true sine, reducing error to the ±1% 5th harmonic squiggle shown in Figure 3. It’s interesting to note that 1% sine accuracy is similar to the performance of the famous Intersil ICL8038 function generator chip. But that was achieved only after in-circuit trimming. The circuit in Figure 1 needs none. Not to brag.
 |
|
| Figure 3. | Imposing trapezoidal truncation of triangle at ±67% prior to integration reduces peak sine error to less than ±1% of mainly 5th harmonic. |
Integration now occurs in A4, with the DC restoration R9C3 network providing zero stability, and R2 controlling sine amplitude.
This last is an important feature because the fact that the sine waveshape results from an integration makes its amplitude inherently inversely proportional to frequency. Therefore, because frequency is unaffected by the sine amplitude adjustment but not vice-versa, the most efficient way to set these two parameters is to adjust frequency first, then set sine amplitude as required. This avoids a potentially time wasting (and frustrating) iteration.
A final comment on Figure 1’s circuit: The TLV9064 is particularly suited for the A1 comparator and the A3 clipper because of its remarkably fast 200 ns overload recovery time. This is unusual performance for an op-amp, particularly such a low power one as the 9064.