Analog Dialogue

Question:
I have heard that it is possible for a gyroscope heading to accumulate drift error over time. Can this happen in my IMU?
Answer:
A MEMS gyroscope, which measures angular rate, has several internal contributors to error, with bias instability as one component. However, an inertial measurement unit (IMU) has several advantages over a discrete component that provides it enhanced performance. An IMU with six degrees of freedom is composed of multiple inertial MEMS sensors that are temperature compensated and calibrated to align on orthogonal axes. The internal 3-axis gyroscope capability measures rotation about a known point while a 3-axis accelerometer measures displacement. A postprocessing step using a digital signal processor or microcontroller provides an internal means for sensor fusion.
Gyroscopes are subject to bias instabilities, in which the initial zero reading of the gyroscope will cause drift over time due to integration of inherent imperfections and noise within the device. Bias repeatability can be calibrated across the known temperature range of the IMU. However, integrating constant bias instability will cause angular error. These errors will accumulate as gyroscope-based rotation or angle estimates drift over the long-term. The undesirable result of drift is that the error of a computed heading increases continuously unabated. Accelerometers, conversely, are sensitive to vibration and other nongravity accelerations.
The gyroscope drift is mainly due to the integration of two components: a slow changing, near-dc variable called bias instability and a higher frequency noise variable called angular random walk (ARW). These parameters are measured in degrees of rotation per unit of time. The yaw axis is most sensitive to this drift. A good portion of the pitch (attitude) and roll axis gyroscope drift can be removed within an IMU through the use of accelerometer feedback to monitor position relative to gravity. Filtering the gyroscope output within an IMU using a low-pass or Kalman filter is also a widely used method to cancel a portion of the drift error.
Ideally, two references are needed to correct for gyroscope drift on all axes. An IMU with nine degrees of freedom typically provides additional magnetometer sensors – about 3 axes. A magnetometer senses field strength relative to the Earth’s magnetic north. These sensors can be used together with accelerometer data, as another external reference, to mitigate the impact of gyroscope drift error on the yaw axis. However, design of proper spatial magnetometers can be a less reliable vector than an accelerometer, as there are many things that create magnetic fields within the same order of magnitude as that of the Earth.
Another one of the more effective methods for canceling long-term drift is to implement a zero angular velocity update to the gyroscope. Any time the device is known to be completely stationary, the gyroscope offset can be nulled to zero for that respective axis. This opportunity can vary wildly depending on the application. But any instance that the system is at a recurring resting state can be used for nulling, such as an idling car, a stationary autonomous robot, or the time between human foot steps.
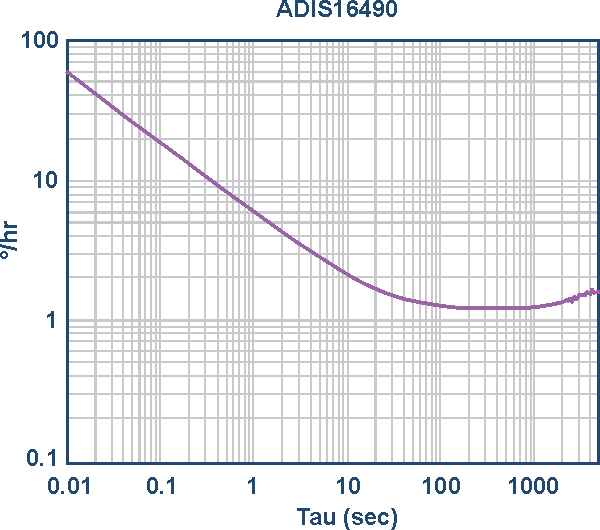 |
||
| Figure 1. | ADIS16490 gyroscope root Allan variance. | |
Of course, using a state-of-the-art IMU that has minimal bias instability within the design at the onset may offer the most immediate impact on gyroscope drift. The constant bias error of a gyroscope can be measured by taking the average of the output over a long period of time while the device is not rotating. An IMU Allan variance plot shows the gyroscope drift in rotational degrees per hour vs. the integration time, Tau. It is normally plotted on a log-log scale. The ADIS16490 is the latest product within ADI’s portfolio of high performance, tactical grade IMUs. The ADIS16490 has an in-run bias stability of merely 1.8° per hour. This is reflected on the ADIS16490 Allan variance plot in Figure 1, where 1.8° of error is seen at the one hour point (3600 seconds).