Ken Wada
embedded.com
Temperature is one of the most common parameters monitored by an embedded system. There is a wide array of temperature sensors available to achieve this. The sensor types can range from exotic black body detectors to the simpler more mundane resistance type sensors and everything in between. In this article, I will briefly discuss the negative temperature coefficient (NTC) thermistor — one of the most common temperature sensors used in a wide variety of embedded systems.
Thermistors
А thermistor is a resistance element, usually made from a polymer or semiconductor, where the resistance varies with respect to the temperature. This type of device should not be confused with a resistance temperature detector (RTD). Usually RTDs are much more precise, more expensive, and cover a wider temperature range.
There are two types of thermistors, characterized by how the resistance varies with temperature. If the resistance value lowers with increasing temperature, we call this device a Negative Temperature Coefficient (NTC) thermistor. If the resistance rises with increasing temperature, this device is known as a Positive Temperature Coefficient (PTC) thermistor. In general, PTC devices are used as protection devices and NTC devices are used as thermal sensors. A very common application of NTC thermistors is in sensing and controlling the PN junction of a wide-band laser diode.
Another characteristic of the thermistor is the cost. A typical thermistor in low volume is usually priced in the $.05 to $0.10 per piece range. The low cost and ease of interface usually make these devices highly attractive in embedded applications.
A typical thermistor sensing range is from -50 to +125 Celsius. Most thermistor-based applications are used in the -10 to 70 Celsius, or what we know as the typical commercial ambient range.
The typical accuracy of the thermistor is average to fair. Most thermistors are manufactured to yield a ±5% resistance tolerance. The precision of a thermistor, however, is pretty decent. Typically, we can expect to see precision on the order of ±0.5 to ±1.0%.
The resistance transfer equation for the thermistor is known as the Steinhart-Hart equation. This non-linear equation is shown as Equation 1.
|
||||
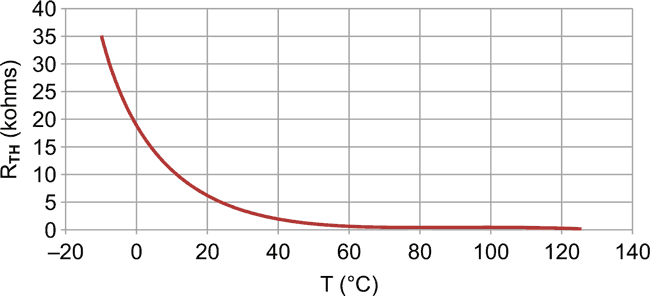
Figure 1 shows the temperature versus resistance plot for a Panasonic ERTJZET472 NTC thermistor. This graph shows that, on a linear scale, the resistance vs. temperature relationship is very nonlinear!
 |
|
| Figure 1. | Resistance vs. Temperature for a Panasonic NTC thermistor. |
Typically, the thermistors are rated by a parameter known as the R25 value. This is the typical resistance of the thermistor at 25 Celsius. The R25 value for this thermistor is 4700 ohms.
We could easily source the thermistor with a low value current source. We could then read the voltage using an on-chip analog-to-digital converter (ADC) and push the read result through some lookup table to get the temperature reading — or we could attempt to linearize the resistance / temperature characteristic.
On some memory constrained systems, we just may not have the luxury of setting up a lookup table. Therefore, in this application we shall attempt to linearize the thermistor reading.
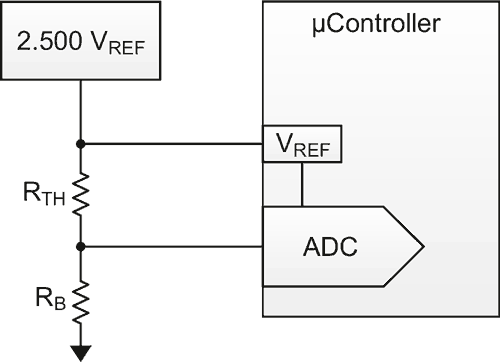
To a first-order approximation, we can see that the thermistor resistance versus temperature characteristic is roughly inversely proportional. That is the resistance is roughly inversely proportional with respect to temperature in a narrow range. Given this, we can create an inverse proportion circuit to try to linearize the resistance vs. temperature curve. Figure 2 shows how this is done.
 |
|
| Figure 2. | An NTC thermistor linearizing circuit. |
If we really wanted to save money, we could eliminate the voltage reference. Doing this will require some extra filtration to reject any power supply noise. It is important that the ADC reference and the thermistor sensor circuit reference are the same. Doing this allows us to use a ratiometric measurement method for the thermistor versus the ADC reading: That is, the measurement will be independent of the excitation voltage of the thermistor interface circuit.
The temperature reading is dependent only on the bias resistor, (RB) and the thermistor resistance, (RTH). We can call this ratio the divider ratio (D). The equation for the divider ratio is the simple voltage divider equation as shown in Equation 2.
|
||||
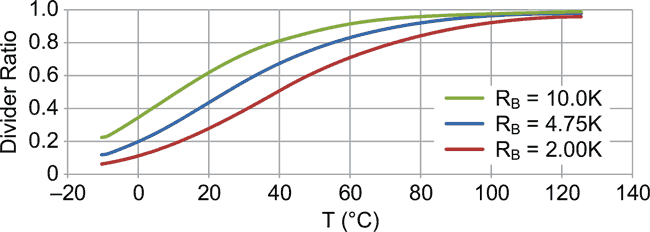
Figure 3 shows a set of curves for the various bias resistor values for the thermistor linearizing circuit. This figure also shows a reasonable degree of linearity within the 0 to 70 Celsius range, with the best linearity being achieved using a lower value of the bias resistor.
 |
|
| Figure 3. | A plot of the divider ratio vs T for various bias resistor values. |
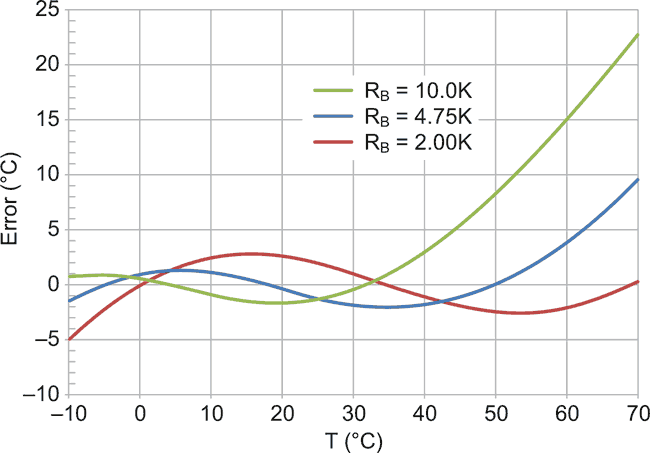
Another, better way to look at this would be to plot the difference between the datasheet values for temperature and the linearized values. This plot is shown in Figure 4. This figure also shows the best linearity is achieved with the lower bias resistor value. This figure shows that a 2.00 Kohm bias resistor will yield a linearity of about ±3 degree Celsius over the 0 to 70 degree temperature range.
 |
|
| Figure 4. | Relative errors for various bias resistor values. |
In this example, the linear equation for the temperature versus resistance ratio, for a 2 Kohm bias resistor is given in Equation 3.
|
||||
Where:
T = temperature in Celsius
D = resistance ratio
We are sourcing the resistance divider and the ADC with the same reference voltage. Thus, we can readily derive the resistance ratio versus ADC reading. If we assume an N-bit converter, the relationship is shown as Equation 4.
|
||||
Where:
D = Resistance ratio
ADC = A/D converter reading
N = A/D converter resolution (# of bits)
Substituting Equation 4 into Equation 3 will yield the equation that relates the ADC reading to the temperature. This equation is shown as Equation 5.
|
||||
Summary
Sometimes as embedded engineers we are called upon to solve a sensor interface problem. In this article I go over an overview of a simple thermistor temperature sensor circuit and how to linearize the resistance vs. temperature sensor function.
One of the principle advantages of using a thermistor is the cost. Typically these sensors are roughly in the $0.05 to $0.10 range in low quantities. The accuracy for these sensors is OK. Usually the resistance tolerance or the R25 tolerance for these devices is around ±3% to ±5%. Therefore a linearizer circuit that yields a ±3 Celsius non-linearity is probably OK.
Of course, we can always use a higher cost sensor, which should yield a better, more accurate result. Some of these sensor types are as follows:
- PN junction sensors. Low cost, reasonable accuracy
- Temperature sensing ICs. These are usually some variation of the PN junction sensor
- Resistance Temperature Detectors, (RTD). These are usually very accurate and higher cost
- Thermocouples. These usually have a much larger range and are modest cost
- Infrared detectors. These usually measure thermal emissions and convert to temperature
These are but a few of the methods one can use to measure temperature. I may discuss how to use some of these methods in a possible future article.So, how do you measure temperature for your embedded system? As you can see, in this article I give a very low cost method to measure this physical parameter. There are a whole slew of other methods out there too.