Dpot pseudolog + log lookup table = actual logarithmic gain

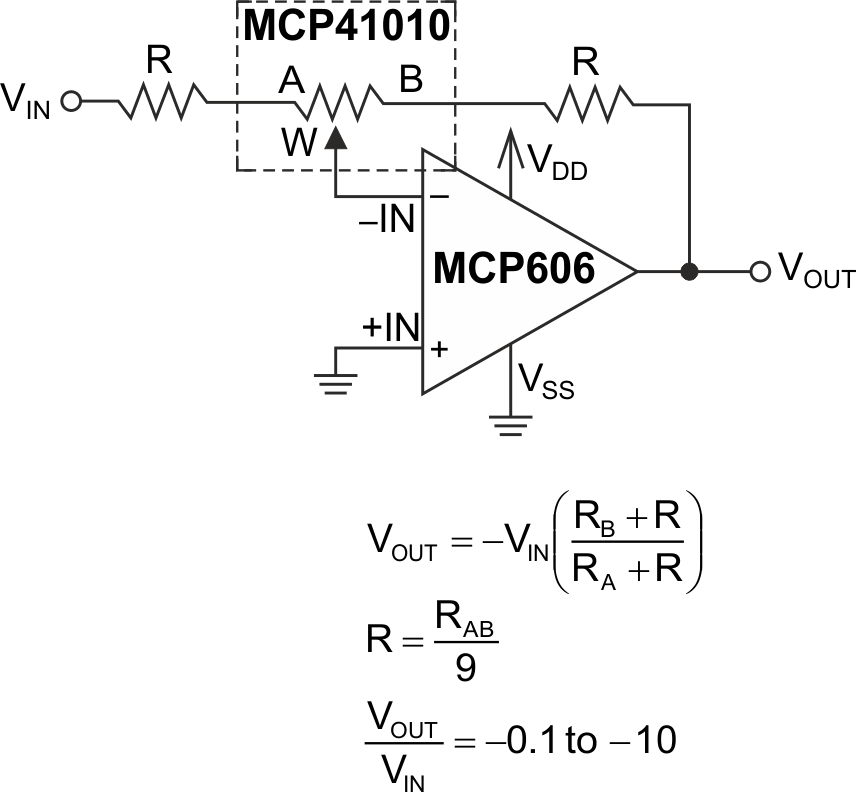
This is the Microchip MCP41xxx digital potentiometer data sheet that includes (on page 15, their Figure 4-4) an interesting application circuit comprising a Dpot controlled amplifier with pseudologarithmic gain settings. However, as explained in the Microchip text, the gains implemented by this circuit start changing radically as the control setting of the pot approaches 0 or 256. As Microchip puts it: “As the wiper approaches either terminal, the step size in the gain calculation increases dramatically. This circuit is recommended for gains between 0.1 and 10 V/V.”

That’s good advice. Unfortunately, following it would effectively throw away some 48 of the 256 8-bit pot settings, amounting to a loss of nearly 20% of available resolution. The simple modification shown in Figure 1 gets rid of that limitation.

Figure 1.	Two fixed resistors are added to bound the gain range to the recommended limits while keeping full 8-bit resolution.

This results in the gain vs code red curve of Figure 2.

Figure 2.	Somewhat improved pseudologarithmic gain curve from the simple modification shown in Figure 1.

However, despite this improvement, the key term remains pseudologarithmic. It still isn’t a real log function and, in fact, isn’t quantitatively even that close, deviating by almost a factor of two in places. Can we do better? Yes!

The simple (software) trick is to prepare a 257-byte logarithmic lookup table that translates the 0.1 to 10.0 gain range settings to the Dpot codes needed to logarithmically generate those gains.

Let’s call the table index variable J. Then for a 257-byte table of (abs) gains G from 0.1 to 10.0 inclusive,

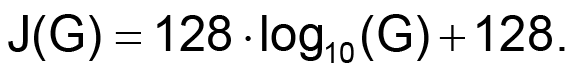
Examples:

J(0.1) = 0,
J(0.5) = 89,
J(1.0) = 128,
J(10.0) = 256,
etc.

Inspection of the gain expression in Figure 1 reveals that the Dpot decimal code N required for (abs) gain G is:

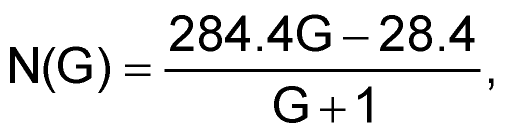
…thus…

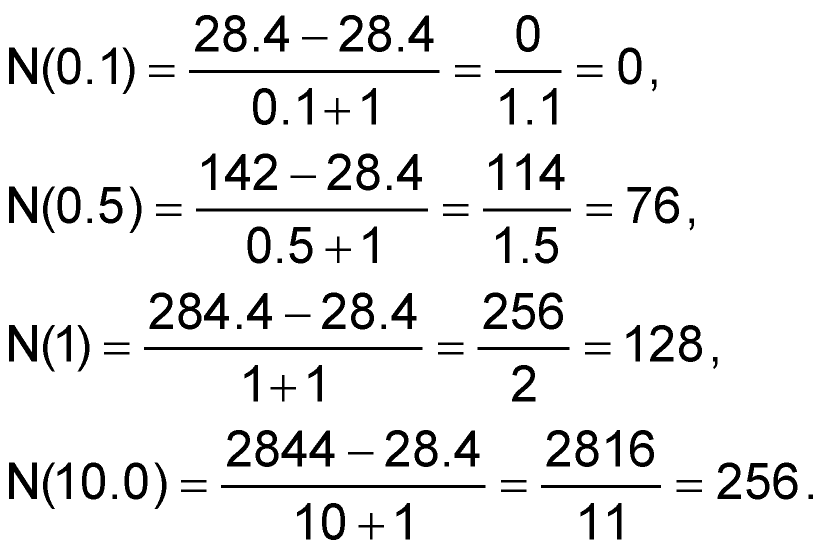
Figure 3 summarizes the resulting relationship between G, J, and N.

Figure 3.	The Dpot settings [N(J)] versus log table indices [J(G)], summarizing the relationship between G, J, and N.

The table of log gains can be found in the Excel sheet (Ref. 1). The net result, with as good log conformity as 8 bits will allow, is exhibited as Figure 4’s lovely green line.

Figure 4.	The absolute gain [GABS = 10(J/128 -1)] versus decimal code (J).

Downloads

1. The Excel sheet

Materials on the topic

1. Datasheet Microchip MCP41XXX/42XXX