Intersil Corporation
Typical resistance accuracy of the polysilicon DCP is in ±20% range. However, the relative accuracy or matching of the resistive elements in the particular resistor array is excellent, and usually is in range of ±1% or better. Thus, this discrepancy between relative and total accuracy should be carefully calculated during the design stage in order to avoid or minimize an additional adjustment of the application circuitry in production. In this application note we will discuss how the DCP accuracy affects the design and some techniques to improve final system accuracy.
There are two major uses of DCP in application design – as a voltage divider and as a variable resistor.
Voltage Divider Mode
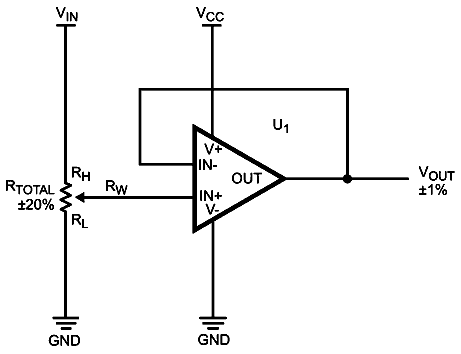 |
|
| Figure 1. | High accuracy voltage divider. |
When a DCP is used as a voltage divider and its RH and RL terminals are connected to the voltage rails, the final accuracy of the wiper RW depends only on the internal resistance matching and will be the same from part to part, regardless of their total resistance accuracy. This is simply because of voltage between RH and RL terminals is divided in between particular number of taps, i.e. scaled down among n numbers of equal resistive elements in the divider string. For example, for the configuration shown in Figure 1, the output voltage VOUT for the wiper position m, can be calculated as Equations 1 and 2.
|
or:
|
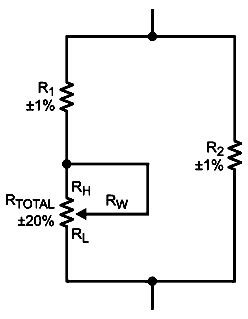
where, m is a current wiper position and n is a total number of taps. As can be seen from Equation 2, the resistance accuracy is canceled out and has no effect on VOUT. However, if a DCP has another resistor(s) on its RH and/or RL terminal, the accuracy of the output signal becomes a function of the initial accuracy of the DCP. This is because the scaled factor is not equal among the divider string, Figure 2.
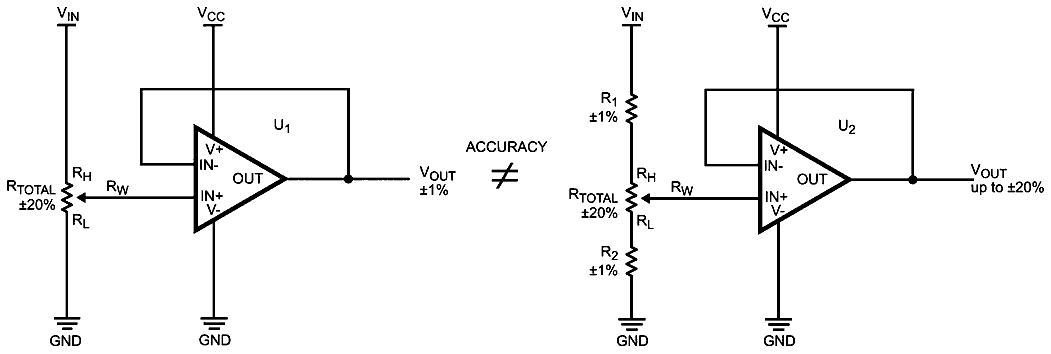 |
|
| Figure 2. | Example of accuracy inequality. |
The output function for the circuitry with R1 and R2 in Figure 2 is as shown in Equation 3:
|
where n is the total number of taps and m is the current wiper position.
Note that wiper resistance is not included, because it has no effect in this particular configuration, assuming that we have an ideal Op Amp.
Rheostat Mode
When a DCP is used as a variable resistor, its output accuracy becomes a combination of initial accuracy (± 20%) plus an additional error from wiper resistance, since the wiper switch is not ideal (it has a small resistance, typically about 70Ω) and its value may vary among the taps. The wiper resistance can be lowered in rheostat configuration, e.g. when the wiper is connected to one of the end terminals (see Figure 3A).
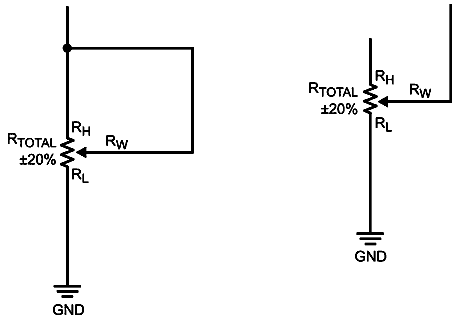 |
|
| а) | б) |
| Figure 3. | Rheostat/variable resistor configuration. |
In rheostat configuration (Figure 3A), wiper resistance appears in parallel with the part of the resistor string and its effect depends on the selected wiper position.
Another possible configuration is to leave one of the end terminals floating as in Figure 3B. In this case, the wiper resistance is well known and usually provided as a graph in a data sheet that makes calculation of total resistance at each tap much easier (Figure 4). Equation 4 can be used to calculate resistance at tap m
|
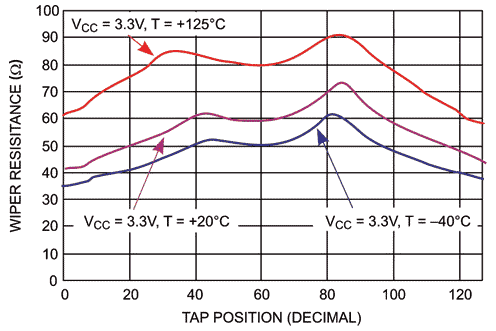 |
|
| Figure 4. | Wiper resistance vs tap position [ I(RW) = VCC/RTOTAL ] for 10kΩ (W). |
Design Examples Allow Increases in Circuitry Accuracy
Even though the initial accuracy of the regular DCP is in ±20% range, the accuracy of the application can be improved by using certain techniques. For example, the design in Figure 2 can be slightly modified in order to get higher accuracy, as shown in Figure 5.
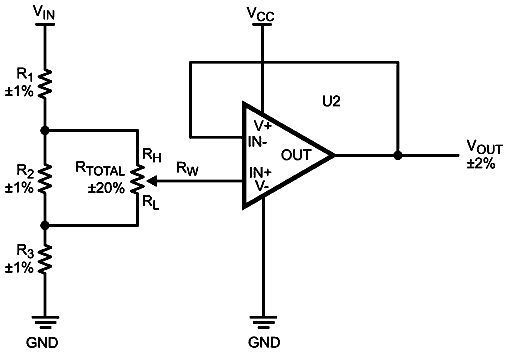 |
|
| Figure 5. | Example of increased accuracy in voltage divider mode. |
In Figure 5, the input signal VIN is divided by the string of fixed resistors R1, R2 and R3, and a DCP is placed in parallel with R2. This configuration preserves the flexibility of the variable output with much higher accuracy. Note that in order to get desired accuracy, the value of RTOTAL has to be about five to ten times the value of R2.
Better accuracy comes when the DCP is used as a variable resistor by combining the DCP with high precision fixed resistors in parallel and serial configuration, Figure 6.
 |
|
| Figure 6. | DCP in both serial and parallel configuration with fixed resistors. |
For example, using 10k 256 taps DCP and circuitry as in Figure 6, we can get a variable resistor from 5.5k to 10.695k with accuracy distributed from ±1.1% to ±8.5%, (Table 1).
| Table 1. | DCP in both serial and parallel configuration with fixed resistors |
|
|
DCP RTOTAL
(kΩ) |
R1
(kΩ) |
R2
(kΩ) |
Minimum total
resistance, DCP at Tap 1 (kΩ) |
Maximum total
resistance, DCP at Tap 255 (kΩ) |
Step resolution
(kΩ) |
Total accuracy
for tap 1 |
Total accuracy
for Tap 255 |
|
Min
|
8
|
6.742
|
29.106
|
5.495
|
9.786
|
0.021
|
–1.08%
|
–8.50%
|
|
Nom
|
10
|
6.81
|
29.4
|
5.555
|
10.695
|
0.026
|
|
|
|
Max
|
12
|
6.878
|
29.694
|
5.615
|
11.541
|
0.031
|
1.08%
|
7.90%
|
There is also the ISL22317, a 1% precision, non-volatile, 128 tap DCP available with the resistance options of 10k, 50k and 100k that can be configured either as a two-terminal variable resistor or as a three-terminal potentiometer. The ISL22317 provides high accuracy, 0Ω of wiper resistance and low temperature coefficient, eliminating the need for complex precision algorithms and other additions.
Another practical usage of the DCPs is an alternative to the DACs. In most cases when the design needs fine tuning within limited range, an 8-bit DCP can achieve even better resolution than a 10-bit DAC. The DCP resolution table as a function of terminal voltages and number of taps is shown in Table 2.
| Table 2. | DCP resolution per tap |
|
Differential
terminal voltages: VH–VL |
Resolution (mV)
|
||||||
|
16 Taps
|
32 Taps
|
64 Taps
|
100 Taps
|
128 Taps
|
256 Taps
|
1024 Taps
|
|
|
4 Bits
|
5 Bits
|
6 Bits
|
7 Bits
|
7 Bits
|
8 Bits
|
10 Bits
|
|
|
10V
|
667
|
323
|
159
|
101
|
79
|
39
|
10
|
|
9V
|
600
|
290
|
143
|
91
|
71
|
35
|
9
|
|
8V
|
533
|
258
|
127
|
81
|
63
|
31
|
8
|
|
7V
|
467
|
226
|
111
|
71
|
55
|
27
|
7
|
|
6V
|
400
|
194
|
95
|
61
|
47
|
24
|
6
|
|
5.5V
|
367
|
177
|
87
|
56
|
43
|
22
|
5
|
|
5V
|
333
|
161
|
79
|
51
|
39
|
20
|
5
|
|
4V
|
267
|
129
|
63
|
40
|
31
|
16
|
4
|
|
3V
|
200
|
97
|
48
|
30
|
24
|
12
|
2.9
|
|
2V
|
133
|
65
|
32
|
20
|
16
|
8
|
2.0
|
|
1V
|
67
|
32
|
16
|
10
|
8
|
3.9
|
1.0
|
|
0.5V
|
33
|
16
|
8
|
5
|
3.9
|
2.0
|
0.5
|
NOTE: Resolution (chart specifies LSB in mV/tap)