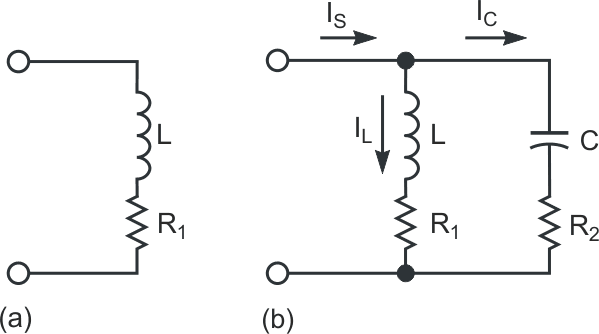
A Zobel network is useful in making a reactive load appear as a pure resistance to a driving source prone to stability problems (Reference 1). A typical situation is an audio power amplifier driving a loudspeaker, modeled at first approximation as an inductance and a series resistor (Figure 1a). The addition of a series R2C network in parallel with the series R1L network forms a Zobel network (Figure 1b). If you select the proper values of R2 and C, the driving source sees a purely resistive load. Reference 2 discusses the computation of the total impedance, ZL, of the Zobel network:
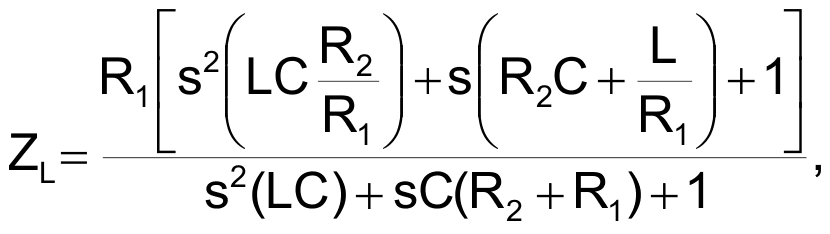
from which you find that the following conditions must prevail:
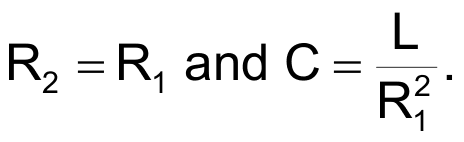
Designing the Zobel network in the time domain, rather than in the transformed-s domain, yields an easier way to arrive at the same result. Moreover, the method provides a better understanding of the reasons why the driver sees a purely resistive load with a Zobel network.
 |
|
| Figure 1. | A first-approximation model of a loudspeaker is an inductance and a resistor in series (a); the addition of a series RC network (b) makes the speaker look purely resistive to the driving source. |
Without loss of generality, let the driving source be an ideal V-volt step-function voltage source. If the load were purely resistive, the source current, IS, would also be a step function. In the absence of the series R2C network, the current flows only through the series R1L load, starting from a zero value and exponentially increasing toward a final value. The time constant in this case is τ1 = L/R1. For the source to supply a step current, you must add another branch that draws a current, IC, such that it compensates for the slow-rising load current, IL. Adding the series R2C network meets that requirement. The current, IC, flowing through that network is instantaneously equal to V/R2 and then decreases exponentially to zero with a time constant τ2 = R2C. For the sum of the current, IL, flowing through the series R1L network and the current IC flowing through the series R2C network to yield a step current IS, R2 must equal R1 and τ2 must equal τ1. That is,
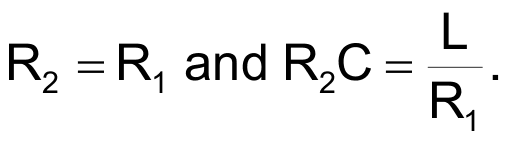
References
- Zobel, OJ, “Distortion Correction in Electrical Circuits with Constant-Resistance Networks,” Bell Systems Technical Journal, July 1982, pg 438.
- Albean, D, “Zobel network tames reactive loads.”
