There are two basic filter topologies that everyone recommends when they start to design their signal chain: multiple-feedback (MFB) or Sallen-Key topologies. But what are the differences and why would you choose one over the other?
MFB filtering
The MFB topology (sometimes called infinite gain or Rauch) is often preferred because it has low sensitivity to amplifier variations, such as the open-loop gain or input range (Figure 1). The MFB topology creates a second-order filter. A MFB single-stage (second-order filter) provides two poles while inverting the signal. In designs where an even number of stages is required, such as a fourth- or eighth-order filter, the output polarity is the same as the input signal. A sixth-order filter consisting of three MFB stages inverts the signal three times, resulting in an inverted output after the third stage. This inversion may or may not be a concern in the application circuit, particularly if you have differential input/output stages.
 |
|
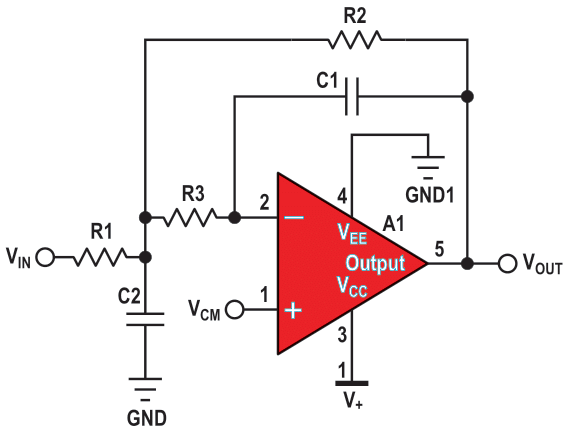
| Figure 1. | MFB second-order single-supply low-pass filter. The gain of this circuit is equal to –R2/R1; VCM = V+/2. |
In Figure 1, the gain circuit is negative and equal to the resistor ratio of R2 and R1. This arrangement allows a variety of negative gains. Generally, the MFB topology allows low sensitivity to component tolerances. The value required for C1 in an MFB design can be quite low while the designer is trying to use reasonable resistor values. The caveat is that low capacitor values can result in significant errors due to parasitic capacitance and the input capacitance of the amplifier.
Sallen-Key filters
 |
|
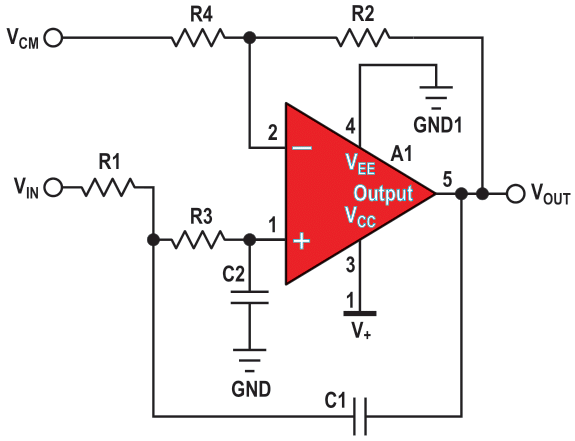
| Figure 2. | Sallen-Key second-order, single-supply filter. The gain of this circuit is 1 +R2/R1; VCM = V+/2. |
There are instances where the Sallen-Key topology is a better choice (Figure 2). A single, second-order Sallen-Key stage also provides two poles but is a non-inverting circuit. This may be preferable over a MFB single stage, but this is not the only potential advantage. As a rule of thumb, the Sallen-Key topology is better if:
- gain accuracy is important, and
- a unity-gain filter is needed, and
- a low Q is required (for example, Q < 3)
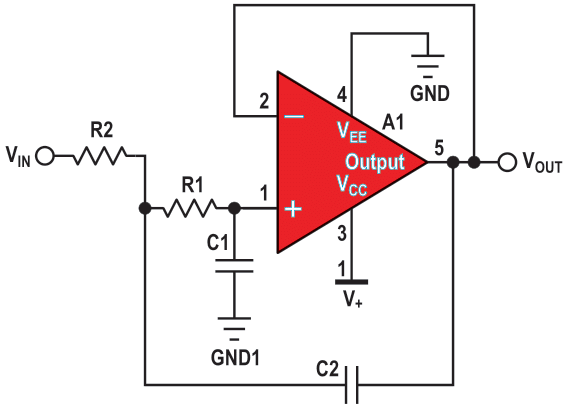
At unity-gain, the Sallen-Key topology has excellent gain accuracy. This is because the op amp is in a unity-gain buffer configuration with a high open-loop gain. Consequently, the gain is independent of the resistors in the circuit. With the MFB topology, the R2/R1 resistor ratio and the resistor errors determine the gain. The unity-gain Sallen-Key topology also requires fewer components – two resistors versus three for the MFB (Figure 3).
 |
|
| Figure 3. | A Sallen-Key second-order, dual-supply, low-pass unity gain filter. The gain of this circuit is equal to 1 V/V. |
Your circuit also may require a low Q, the quality factor. The relationship between Q and the damping factor is Q = ½ζ, where ζ is the damping factor. The higher the Q, the more easily the circuit oscillates, particularly at the 3 dB corner frequency.
The Sallen-Key topology may be preferable for low-Q, high-frequency filter sections.
Selecting the correct amplifier, for these circuits, presents an interesting challenge. It is not simply a matter of picking an amplifier with a gain-bandwidth-product that is 100 times higher than the filter’s corner frequency. The amplifier bandwidth calculation involves variations of the amplifier’s bandwidth and variations of the passive components over time, to mention a few.